scipy.integrate.odeint

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

Integrate a system of ordinary differential equations.

Note

For new code, use scipy.integrate.solve_ivp to solve a differential equation.

Solve a system of ordinary differential equations using lsoda from the FORTRAN library odepack.

Solves the initial value problem for stiff or non-stiff systems of first order ode-s:

dy/dt = func(y, t, ...)  [or func(t, y, ...)]

where y can be a vector.

Note

By default, the required order of the first two arguments of func are in the opposite order of the arguments in the system definition function used by the scipy.integrate.ode class and the function scipy.integrate.solve_ivp. To use a function with the signature func(t, y, ...), the argument tfirst must be set to True.

Parameters:

func : callable(y, t, …) or callable(t, y, …)

Computes the derivative of y at t. If the signature is callable(t, y, ...), then the argument tfirst must be set True.

y0 : array

Initial condition on y (can be a vector).

t : array

A sequence of time points for which to solve for y. The initial value point should be the first element of this sequence. This sequence must be monotonically increasing or monotonically decreasing; repeated values are allowed.

args : tuple, optional

Extra arguments to pass to function.

Dfun : callable(y, t, …) or callable(t, y, …)

Gradient (Jacobian) of func. If the signature is callable(t, y, ...), then the argument tfirst must be set True.

col_deriv : bool, optional

True if Dfun defines derivatives down columns (faster), otherwise Dfun should define derivatives across rows.

full_output : bool, optional

True if to return a dictionary of optional outputs as the second output

printmessg : bool, optional

Whether to print the convergence message

tfirst: bool, optional

If True, the first two arguments of func (and Dfun, if given) must t, y instead of the default y, t.

New in version 1.1.0.

Returns:

y : array, shape (len(t), len(y0))

Array containing the value of y for each desired time in t, with the initial value y0 in the first row.

infodict : dict, only returned if full_output == True

Dictionary containing additional output information

key	meaning
‘hu’	vector of step sizes successfully used for each time step.
‘tcur’	vector with the value of t reached for each time step. (will always be at least as large as the input times).
‘tolsf’	vector of tolerance scale factors, greater than 1.0, computed when a request for too much accuracy was detected.
‘tsw’	value of t at the time of the last method switch (given for each time step)
‘nst’	cumulative number of time steps
‘nfe’	cumulative number of function evaluations for each time step
‘nje’	cumulative number of jacobian evaluations for each time step
‘nqu’	a vector of method orders for each successful step.
‘imxer’	index of the component of largest magnitude in the weighted local error vector (e / ewt) on an error return, -1 otherwise.
‘lenrw’	the length of the double work array required.
‘leniw’	the length of integer work array required.
‘mused’	a vector of method indicators for each successful time step: 1: adams (nonstiff), 2: bdf (stiff)

Other Parameters:  

ml, mu : int, optional

If either of these are not None or non-negative, then the Jacobian is assumed to be banded. These give the number of lower and upper non-zero diagonals in this banded matrix. For the banded case, Dfun should return a matrix whose rows contain the non-zero bands (starting with the lowest diagonal). Thus, the return matrix jac from Dfun should have shape (ml + mu + 1, len(y0)) when ml >=0 or mu >=0. The data in jac must be stored such that jac[i - j + mu, j] holds the derivative of the i`th equation with respect to the `j`th state variable. If `col_deriv is True, the transpose of this jac must be returned.

rtol, atol : float, optional

The input parameters rtol and atol determine the error control performed by the solver. The solver will control the vector, e, of estimated local errors in y, according to an inequality of the form max-norm of (e / ewt) <= 1, where ewt is a vector of positive error weights computed as ewt = rtol * abs(y) + atol. rtol and atol can be either vectors the same length as y or scalars. Defaults to 1.49012e-8.

tcrit : ndarray, optional

Vector of critical points (e.g. singularities) where integration care should be taken.

h0 : float, (0: solver-determined), optional

The step size to be attempted on the first step.

hmax : float, (0: solver-determined), optional

The maximum absolute step size allowed.

hmin : float, (0: solver-determined), optional

The minimum absolute step size allowed.

ixpr : bool, optional

Whether to generate extra printing at method switches.

mxstep : int, (0: solver-determined), optional

Maximum number of (internally defined) steps allowed for each integration point in t.

mxhnil : int, (0: solver-determined), optional

Maximum number of messages printed.

mxordn : int, (0: solver-determined), optional

Maximum order to be allowed for the non-stiff (Adams) method.

mxords : int, (0: solver-determined), optional

Maximum order to be allowed for the stiff (BDF) method.

See also

solve_ivp

Solve an initial value problem for a system of ODEs.

ode

a more object-oriented integrator based on VODE.

quad

for finding the area under a curve.

Examples

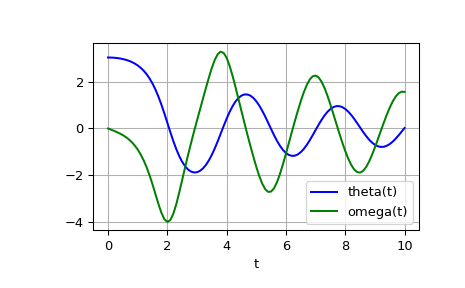
The second order differential equation for the angle theta of a pendulum acted on by gravity with friction can be written:

theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0

where b and c are positive constants, and a prime (‘) denotes a derivative. To solve this equation with odeint, we must first convert it to a system of first order equations. By defining the angular velocity omega(t) = theta'(t), we obtain the system:

theta'(t) = omega(t)
omega'(t) = -b*omega(t) - c*sin(theta(t))

Let y be the vector [theta, omega]. We implement this system in python as:

>>> def pend(y, t, b, c):
...     theta, omega = y
...     dydt = [omega, -b*omega - c*np.sin(theta)]
...     return dydt
...

We assume the constants are b = 0.25 and c = 5.0:

>>> b = 0.25
>>> c = 5.0

For initial conditions, we assume the pendulum is nearly vertical with theta(0) = pi - 0.1, and is initially at rest, so omega(0) = 0. Then the vector of initial conditions is

>>> y0 = [np.pi - 0.1, 0.0]

We will generate a solution at 101 evenly spaced samples in the interval 0 <= t <= 10. So our array of times is:

>>> t = np.linspace(0, 10, 101)

Call odeint to generate the solution. To pass the parameters b and c to pend, we give them to odeint using the args argument.

>>> from scipy.integrate import odeint
>>> sol = odeint(pend, y0, t, args=(b, c))

The solution is an array with shape (101, 2). The first column is theta(t), and the second is omega(t). The following code plots both components.

>>> import matplotlib.pyplot as plt
>>> plt.plot(t, sol[:, 0], 'b', label='theta(t)')
>>> plt.plot(t, sol[:, 1], 'g', label='omega(t)')
>>> plt.legend(loc='best')
>>> plt.xlabel('t')
>>> plt.grid()
>>> plt.show()