scipy.stats.

make_distribution

scipy.stats.make_distribution(dist)

Generate a UnivariateDistribution class from a compatible object

The argument may be an instance of rv_continuous or an instance of another class that satisfies the interface described below.

The returned value is a ContinuousDistribution subclass if the input is an instance of rv_continuous or a DiscreteDistribution subclass if the input is an instance of rv_discrete. Like any subclass of UnivariateDistribution, it must be instantiated (i.e. by passing all shape parameters as keyword arguments) before use. Once instantiated, the resulting object will have the same interface as any other instance of UnivariateDistribution; e.g., scipy.stats.Normal, scipy.stats.Binomial.

Note

make_distribution does not work perfectly with all instances of rv_continuous. Known failures include levy_stable, vonmises, hypergeom, ‘nchypergeom_fisher’, ‘nchypergeom_wallenius’, and poisson_binom. Some methods of some distributions will not support array shape parameters.

Parameters:

distrv_continuous

Instance of rv_continuous, rv_discrete, or an instance of any class with the following attributes:

__make_distribution_version__str

A string containing the version number of SciPy in which this interface is defined. The preferred interface may change in future SciPy versions, in which case support for an old interface version may be deprecated and eventually removed.

parametersdict or tuple

If a dictionary, each key is the name of a parameter, and the corresponding value is either a dictionary or tuple. If the value is a dictionary, it may have the following items, with default values used for entries which aren’t present.

endpointstuple, default: (-inf, inf)

A tuple defining the lower and upper endpoints of the domain of the parameter; allowable values are floats, the name (string) of another parameter, or a callable taking parameters as keyword only arguments and returning the numerical value of an endpoint for given parameter values.

inclusivetuple of bool, default: (False, False)

A tuple specifying whether the endpoints are included within the domain of the parameter.

typicaltuple, default: endpoints

Defining endpoints of a typical range of values of a parameter. Can be used for sampling parameter values for testing. Behaves like the endpoints tuple above, and should define a subinterval of the domain given by endpoints.

A tuple value (a, b) associated to a key in the parameters dictionary is equivalent to {endpoints: (a, b)}.

Custom distributions with multiple parameterizations can be defined by having the parameters attribute be a tuple of dictionaries with the structure described above. In this case, dist’s class must also define a method process_parameters to map between the different parameterizations. It must take all parameters from all parameterizations as optional keyword arguments and return a dictionary mapping parameters to values, filling in values from other parameterizations using values from the supplied parameterization. See example.

supportdict or tuple

A dictionary describing the support of the distribution or a tuple describing the endpoints of the support. This behaves identically to the values of the parameters dict described above, except that the key typical is ignored.

The class must also define a pdf method and may define methods logentropy, entropy, median, mode, logpdf, logcdf, cdf, logccdf, ccdf, ilogcdf, icdf, ilogccdf, iccdf, moment, and sample. If defined, these methods must accept the parameters of the distribution as keyword arguments and also accept any positional-only arguments accepted by the corresponding method of ContinuousDistribution. When multiple parameterizations are defined, these methods must accept all parameters from all parameterizations. The moment method must accept the order and kind arguments by position or keyword, but may return None if a formula is not available for the arguments; in this case, the infrastructure will fall back to a default implementation. The sample method must accept shape by position or keyword, but contrary to the public method of the same name, the argument it receives will be the full shape of the output array - that is, the shape passed to the public method prepended to the broadcasted shape of random variable parameters.

Returns:

CustomDistributionUnivariateDistribution

A subclass of UnivariateDistribution corresponding with dist. The initializer requires all shape parameters to be passed as keyword arguments (using the same names as the instance of rv_continuous/rv_discrete).

Notes

The documentation of UnivariateDistribution is not rendered. See below for an example of how to instantiate the class (i.e. pass all shape parameters of dist to the initializer as keyword arguments). Documentation of all methods is identical to that of scipy.stats.Normal. Use help on the returned class or its methods for more information.

Examples

Try it in your browser!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> from scipy import special

Create a ContinuousDistribution from scipy.stats.loguniform.

>>> LogUniform = stats.make_distribution(stats.loguniform)
>>> X = LogUniform(a=1.0, b=3.0)
>>> np.isclose((X + 0.25).median(), stats.loguniform.ppf(0.5, 1, 3, loc=0.25))
np.True_
>>> X.plot()
>>> sample = X.sample(10000, rng=np.random.default_rng())
>>> plt.hist(sample, density=True, bins=30)
>>> plt.legend(('pdf', 'histogram'))
>>> plt.show()

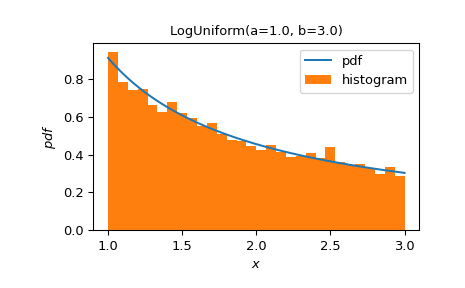
Create a custom distribution.

>>> class MyLogUniform:
...     @property
...     def __make_distribution_version__(self):
...         return "1.16.0"
...
...     @property
...     def parameters(self):
...         return {'a': {'endpoints': (0, np.inf),
...                       'inclusive': (False, False)},
...                 'b': {'endpoints': ('a', np.inf),
...                       'inclusive': (False, False)}}
...
...     @property
...     def support(self):
...         return {'endpoints': ('a', 'b'), 'inclusive': (True, True)}
...
...     def pdf(self, x, a, b):
...         return 1 / (x * (np.log(b)- np.log(a)))
>>>
>>> MyLogUniform = stats.make_distribution(MyLogUniform())
>>> Y = MyLogUniform(a=1.0, b=3.0)
>>> np.isclose(Y.cdf(2.), X.cdf(2.))
np.True_

Create a custom distribution with variable support.

>>> class MyUniformCube:
...     @property
...     def __make_distribution_version__(self):
...         return "1.16.0"
...
...     @property
...     def parameters(self):
...         return {"a": (-np.inf, np.inf),
...                 "b": {'endpoints':('a', np.inf), 'inclusive':(True, False)}}
...
...     @property
...     def support(self):
...         def left(*, a, b):
...             return a**3
...
...         def right(*, a, b):
...             return b**3
...         return (left, right)
...
...     def pdf(self, x, *, a, b):
...         return 1 / (3*(b - a)*np.cbrt(x)**2)
...
...     def cdf(self, x, *, a, b):
...         return (np.cbrt(x) - a) / (b - a)
>>>
>>> MyUniformCube = stats.make_distribution(MyUniformCube())
>>> X = MyUniformCube(a=-2, b=2)
>>> Y = stats.Uniform(a=-2, b=2)**3
>>> X.support()
(-8.0, 8.0)
>>> np.isclose(X.cdf(2.1), Y.cdf(2.1))
np.True_

Create a custom distribution with multiple parameterizations. Here we create a custom version of the beta distribution that has an alternative parameterization in terms of the mean mu and a dispersion parameter nu.

>>> class MyBeta:
...     @property
...     def __make_distribution_version__(self):
...         return "1.16.0"
...
...     @property
...     def parameters(self):
...         return ({"a": (0, np.inf), "b": (0, np.inf)},
...                 {"mu": (0, 1), "nu": (0, np.inf)})
...
...     def process_parameters(self, a=None, b=None, mu=None, nu=None):
...         if a is not None and b is not None:
...             nu = a + b
...             mu = a / nu
...         else:
...             a = mu * nu
...             b = nu - a
...         return dict(a=a, b=b, mu=mu, nu=nu)
...
...     @property
...     def support(self):
...         return {'endpoints': (0, 1)}
...
...     def pdf(self, x, a, b, mu, nu):
...         return special._ufuncs._beta_pdf(x, a, b)
...
...     def cdf(self, x, a, b, mu, nu):
...         return special.betainc(a, b, x)
>>>
>>> MyBeta = stats.make_distribution(MyBeta())
>>> X = MyBeta(a=2.0, b=2.0)
>>> Y = MyBeta(mu=0.5, nu=4.0)
>>> np.isclose(X.pdf(0.3), Y.pdf(0.3))
np.True_

Go BackOpen In Tab