Shapiro-Wilk test for normality#
Suppose we wish to infer from measurements whether the weights of adult human
males in a medical study are not normally distributed [1]. The weights (lbs)
are recorded in the array x below.
import numpy as np
x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])
The normality test scipy.stats.shapiro of [1] and [2] begins by
computing a statistic based on the relationship between the observations and the
expected order statistics of a normal distribution.
from scipy import stats
res = stats.shapiro(x)
res.statistic
0.7888146948631716
The value of this statistic tends to be high (close to 1) for samples drawn from a normal distribution.
The test is performed by comparing the observed value of the statistic against
the null distribution: the distribution of statistic values formed under the
null hypothesis that the weights were drawn from a normal distribution. For this
normality test, the null distribution is not easy to calculate exactly, so it is
usually approximated by Monte Carlo methods, that is, drawing many samples of
the same size as x from a normal distribution and computing the values of the
statistic for each.
def statistic(x):
# Get only the `shapiro` statistic; ignore its p-value
return stats.shapiro(x).statistic
ref = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
alternative='less')
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 5))
bins = np.linspace(0.65, 1, 50)
def plot(ax): # we'll reuse this
ax.hist(ref.null_distribution, density=True, bins=bins)
ax.set_title("Shapiro-Wilk Test Null Distribution \n"
"(Monte Carlo Approximation, 11 Observations)")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
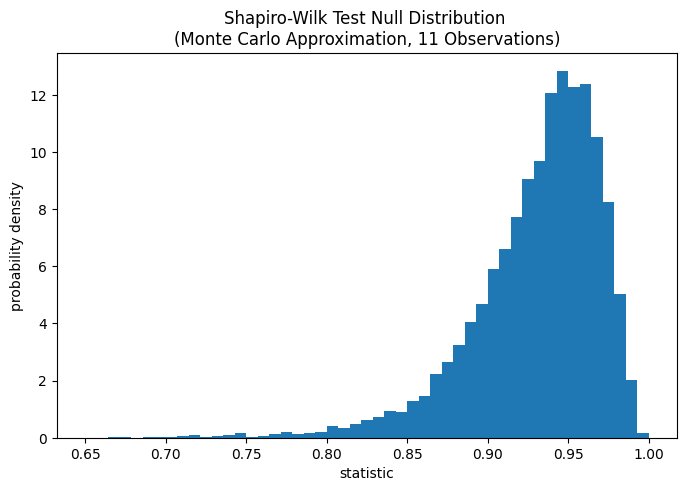
The comparison is quantified by the p-value: the proportion of values in the null distribution less than or equal to the observed value of the statistic.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
annotation = (f'p-value={res.pvalue:.6f}\n(highlighted area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (0.75, 0.1), (0.68, 0.7), arrowprops=props)
i_extreme = np.where(bins <= res.statistic)[0]
for i in i_extreme:
ax.patches[i].set_color('C1')
plt.xlim(0.65, 0.9)
plt.ylim(0, 4)
plt.show()
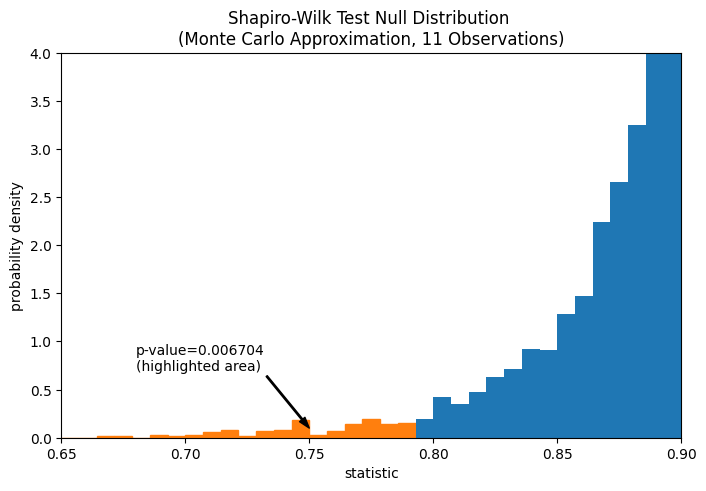
res.pvalue
0.006703814061898823
If the p-value is “small” - that is, if there is a low probability of sampling data from a normally distributed population that produces such an extreme value of the statistic - this may be taken as evidence against the null hypothesis in favor of the alternative: the weights were not drawn from a normal distribution. Note that:
The inverse is not true; that is, the test is not used to provide evidence for the null hypothesis.
The threshold for values that will be considered “small” is a choice that should be made before the data is analyzed [3] with consideration of the risks of both false positives (incorrectly rejecting the null hypothesis) and false negatives (failure to reject a false null hypothesis).