Kendall’s tau test#
Kendall’s tau is a measure of the correspondence between two rankings.
Consider the following data from [1], which studied the relationship between free proline (an amino acid) and total collagen (a protein often found in connective tissue) in unhealthy human livers.
The x and y arrays below record measurements of the two compounds. The
observations are paired: each free proline measurement was taken from the same
liver as the total collagen measurement at the same index.
import numpy as np
# total collagen (mg/g dry weight of liver)
x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
# free proline (μ mole/g dry weight of liver)
y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])
These data were analyzed in [2] using Spearman’s correlation coefficient,
a statistic similar to Kendall’s tau in that it is also sensitive to
ordinal correlation between the samples. Let’s perform an analogous study
using Kendall's tau.
from scipy import stats
res = stats.kendalltau(x, y)
res.statistic
0.5499999999999999
The value of this statistic tends to be high (close to 1) for samples with a strongly positive ordinal correlation, low (close to -1) for samples with a strongly negative ordinal correlation, and small in magnitude (close to zero) for samples with weak ordinal correlation.
The test is performed by comparing the observed value of the statistic against the null distribution: the distribution of statistic values derived under the null hypothesis that total collagen and free proline measurements are independent.
For this test, the null distribution for large samples without ties is
approximated as the normal distribution with variance
(2*(2*n + 5))/(9*n*(n - 1)), where n = len(x).
import matplotlib.pyplot as plt
n = len(x) # len(x) == len(y)
var = (2*(2*n + 5))/(9*n*(n - 1))
dist = stats.norm(scale=np.sqrt(var))
z_vals = np.linspace(-1.25, 1.25, 100)
pdf = dist.pdf(z_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(z_vals, pdf)
ax.set_title("Kendall Tau Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
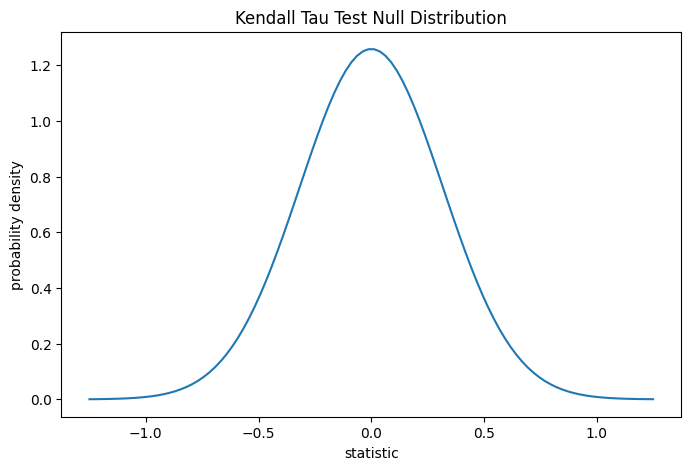
The comparison is quantified by the p-value: the proportion of values in the null distribution as extreme or more extreme than the observed value of the statistic. In a two-sided test in which the statistic is positive, elements of the null distribution greater than the transformed statistic and elements of the null distribution less than the negative of the observed statistic are both considered “more extreme”.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (0.65, 0.15), (0.8, 0.3), arrowprops=props)
i = z_vals >= res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
i = z_vals <= -res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-1.25, 1.25)
ax.set_ylim(0, 0.5)
plt.show()
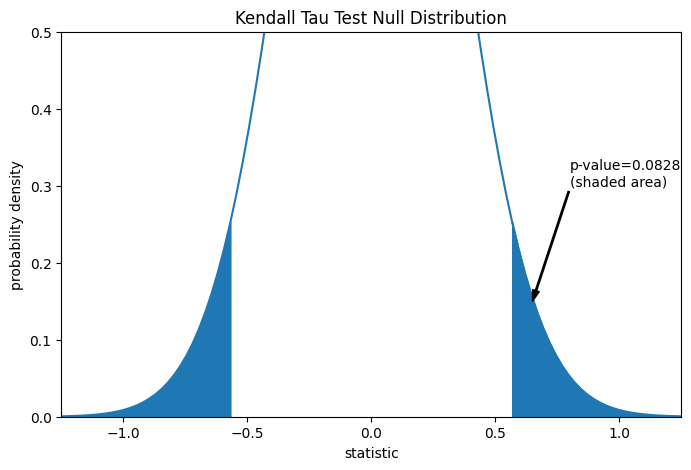
res.pvalue
0.09108705741631495
Note that there is slight disagreement between the shaded area of the curve and
the p-value returned by scipy.stats.kendalltau. This is because our data
has ties, and we have neglected a tie correction to the null distribution
variance that scipy.stats.kendalltau performs. For samples without ties,
the shaded areas of our plot and p-value returned by
scipy.stats.kendalltau would match exactly.
If the p-value is “small” - that is, if there is a low probability of sampling data from independent distributions that produces such an extreme value of the statistic - this may be taken as evidence against the null hypothesis in favor of the alternative: the distribution of total collagen and free proline are not independent. Note that:
The inverse is not true; that is, the test is not used to provide evidence for the null hypothesis.
The threshold for values that will be considered “small” is a choice that should be made before the data is analyzed [3] with consideration of the risks of both false positives (incorrectly rejecting the null hypothesis) and false negatives (failure to reject a false null hypothesis).
Small p-values are not evidence for a large effect; rather, they can only provide evidence for a “significant” effect, meaning that they are unlikely to have occurred under the null hypothesis.
For samples without ties of moderate size, scipy.stats.kendalltau can
compute the p-value exactly. However, in the presence of ties,
scipy.stats.kendalltau resorts to an asymptotic approximation.
Nonetheless, we can use a permutation test to compute the null distribution
exactly: Under the null hypothesis that total collagen and free proline are
independent, each of the free proline measurements were equally likely to have
been observed with any of the total collagen measurements. Therefore, we can
form an exact null distribution by calculating the statistic under each
possible pairing of elements between x and y.
def statistic(x): # explore all possible pairings by permuting `x`
return stats.kendalltau(x, y).statistic # ignore pvalue
ref = stats.permutation_test((x,), statistic,
permutation_type='pairings')
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(-1.25, 1.25, 25)
ax.hist(ref.null_distribution, bins=bins, density=True)
ax.legend(['asymptotic approximation\n(many observations)',
'exact null distribution'])
plot(ax)
plt.show()
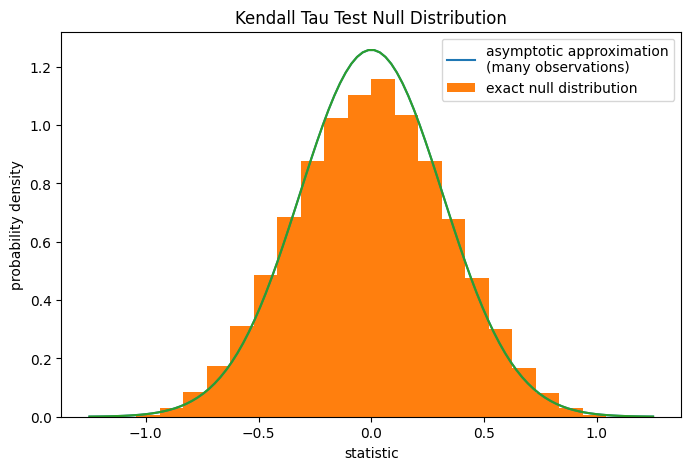
ref.pvalue
0.12222222222222222
Note that there is significant disagreement between the exact p-value calculated
here and the approximation returned by scipy.stats.kendalltau above. For
small samples with ties, consider performing a permutation test for more
accurate results.