MultinomialQMC#
- class scipy.stats.qmc.MultinomialQMC(pvals, n_trials, *, engine=None, rng=None)[source]#
QMC sampling from a multinomial distribution.
- Parameters:
- pvalsarray_like (k,)
Vector of probabilities of size
k, wherekis the number of categories. Elements must be non-negative and sum to 1.- n_trialsint
Number of trials.
- engineQMCEngine, optional
Quasi-Monte Carlo engine sampler. If None,
Sobolis used.- rng
numpy.random.Generator, optional Pseudorandom number generator state. When rng is None, a new
numpy.random.Generatoris created using entropy from the operating system. Types other thannumpy.random.Generatorare passed tonumpy.random.default_rngto instantiate aGenerator.Changed in version 1.15.0: As part of the SPEC-007 transition from use of
numpy.random.RandomStatetonumpy.random.Generator, this keyword was changed from seed to rng. For an interim period, both keywords will continue to work, although only one may be specified at a time. After the interim period, function calls using the seed keyword will emit warnings. Following a deprecation period, the seed keyword will be removed.
Examples
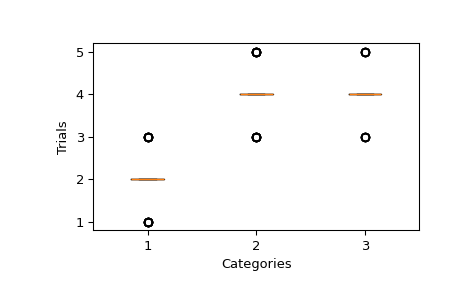
Let’s define 3 categories and for a given sample, the sum of the trials of each category is 8. The number of trials per category is determined by the pvals associated to each category. Then, we sample this distribution 64 times.
>>> import matplotlib.pyplot as plt >>> from scipy.stats import qmc >>> dist = qmc.MultinomialQMC( ... pvals=[0.2, 0.4, 0.4], n_trials=10, engine=qmc.Halton(d=1) ... ) >>> sample = dist.random(64)
We can plot the sample and verify that the median of number of trials for each category is following the pvals. That would be
pvals * n_trials = [2, 4, 4].>>> fig, ax = plt.subplots() >>> ax.yaxis.get_major_locator().set_params(integer=True) >>> _ = ax.boxplot(sample) >>> ax.set(xlabel="Categories", ylabel="Trials") >>> plt.show()
Methods
random([n])Draw n QMC samples from the multinomial distribution.