RegularGridInterpolator#
- class scipy.interpolate.RegularGridInterpolator(points, values, method='linear', bounds_error=True, fill_value=nan, *, solver=None, solver_args=None)[source]#
Interpolator on a regular or rectilinear grid in arbitrary dimensions.
The data must be defined on a rectilinear grid; that is, a rectangular grid with even or uneven spacing. Linear, nearest-neighbor, spline interpolations are supported. After setting up the interpolator object, the interpolation method may be chosen at each evaluation.
- Parameters:
- pointstuple of ndarray of float, with shapes (m1, ), …, (mn, )
The points defining the regular grid in n dimensions. The points in each dimension (i.e. every elements of the points tuple) must be strictly ascending or descending.
- valuesarray_like, shape (m1, …, mn, …)
The data on the regular grid in n dimensions. Complex data is accepted.
- methodstr, optional
The method of interpolation to perform. Supported are “linear”, “nearest”, “slinear”, “cubic”, “quintic” and “pchip”. This parameter will become the default for the object’s
__call__method. Default is “linear”.- bounds_errorbool, optional
If True, when interpolated values are requested outside of the domain of the input data, a ValueError is raised. If False, then fill_value is used. Default is True.
- fill_valuefloat or None, optional
The value to use for points outside of the interpolation domain. If None, values outside the domain are extrapolated. Default is
np.nan.- solvercallable, optional
Only used for methods “slinear”, “cubic” and “quintic”. Sparse linear algebra solver for construction of the NdBSpline instance. Default is the iterative solver
scipy.sparse.linalg.gcrotmk.Added in version 1.13.
- solver_args: dict, optional
Additional arguments to pass to solver, if any.
Added in version 1.13.
See also
NearestNDInterpolatorNearest neighbor interpolator on unstructured data in N dimensions
LinearNDInterpolatorPiecewise linear interpolator on unstructured data in N dimensions
interpna convenience function which wraps
RegularGridInterpolatorscipy.ndimage.map_coordinatesinterpolation on grids with equal spacing (suitable for e.g., N-D image resampling)
Notes
Contrary to
LinearNDInterpolatorandNearestNDInterpolator, this class avoids expensive triangulation of the input data by taking advantage of the regular grid structure.In other words, this class assumes that the data is defined on a rectilinear grid.
Added in version 0.14.
The ‘slinear’(k=1), ‘cubic’(k=3), and ‘quintic’(k=5) methods are tensor-product spline interpolators, where k is the spline degree, If any dimension has fewer points than k + 1, an error will be raised.
Added in version 1.9.
If the input data is such that dimensions have incommensurate units and differ by many orders of magnitude, the interpolant may have numerical artifacts. Consider rescaling the data before interpolating.
Choosing a solver for spline methods
Spline methods, “slinear”, “cubic” and “quintic” involve solving a large sparse linear system at instantiation time. Depending on data, the default solver may or may not be adequate. When it is not, you may need to experiment with an optional solver argument, where you may choose between the direct solver (
scipy.sparse.linalg.spsolve) or iterative solvers fromscipy.sparse.linalg. You may need to supply additional parameters via the optional solver_args parameter (for instance, you may supply the starting value or target tolerance). See thescipy.sparse.linalgdocumentation for the full list of available options.Alternatively, you may instead use the legacy methods, “slinear_legacy”, “cubic_legacy” and “quintic_legacy”. These methods allow faster construction but evaluations will be much slower.
References
[1]Python package regulargrid by Johannes Buchner, see https://pypi.python.org/pypi/regulargrid/
[2]Wikipedia, “Trilinear interpolation”, https://en.wikipedia.org/wiki/Trilinear_interpolation
[3]Weiser, Alan, and Sergio E. Zarantonello. “A note on piecewise linear and multilinear table interpolation in many dimensions.” MATH. COMPUT. 50.181 (1988): 189-196. https://www.ams.org/journals/mcom/1988-50-181/S0025-5718-1988-0917826-0/S0025-5718-1988-0917826-0.pdf DOI:10.1090/S0025-5718-1988-0917826-0
Examples
Evaluate a function on the points of a 3-D grid
As a first example, we evaluate a simple example function on the points of a 3-D grid:
>>> from scipy.interpolate import RegularGridInterpolator >>> import numpy as np >>> def f(x, y, z): ... return 2 * x**3 + 3 * y**2 - z >>> x = np.linspace(1, 4, 11) >>> y = np.linspace(4, 7, 22) >>> z = np.linspace(7, 9, 33) >>> xg, yg ,zg = np.meshgrid(x, y, z, indexing='ij', sparse=True) >>> data = f(xg, yg, zg)
datais now a 3-D array withdata[i, j, k] = f(x[i], y[j], z[k]). Next, define an interpolating function from this data:>>> interp = RegularGridInterpolator((x, y, z), data)
Evaluate the interpolating function at the two points
(x,y,z) = (2.1, 6.2, 8.3)and(3.3, 5.2, 7.1):>>> pts = np.array([[2.1, 6.2, 8.3], ... [3.3, 5.2, 7.1]]) >>> interp(pts) array([ 125.80469388, 146.30069388])
which is indeed a close approximation to
>>> f(2.1, 6.2, 8.3), f(3.3, 5.2, 7.1) (125.54200000000002, 145.894)
Interpolate and extrapolate a 2D dataset
As a second example, we interpolate and extrapolate a 2D data set:
>>> x, y = np.array([-2, 0, 4]), np.array([-2, 0, 2, 5]) >>> def ff(x, y): ... return x**2 + y**2
>>> xg, yg = np.meshgrid(x, y, indexing='ij') >>> data = ff(xg, yg) >>> interp = RegularGridInterpolator((x, y), data, ... bounds_error=False, fill_value=None)
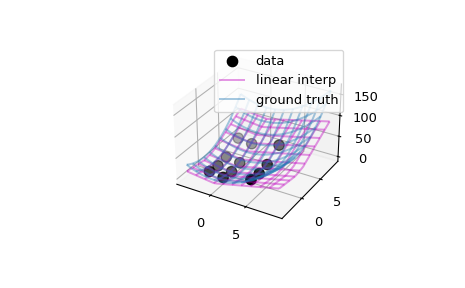
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax = fig.add_subplot(projection='3d') >>> ax.scatter(xg.ravel(), yg.ravel(), data.ravel(), ... s=60, c='k', label='data')
Evaluate and plot the interpolator on a finer grid
>>> xx = np.linspace(-4, 9, 31) >>> yy = np.linspace(-4, 9, 31) >>> X, Y = np.meshgrid(xx, yy, indexing='ij')
>>> # interpolator >>> ax.plot_wireframe(X, Y, interp((X, Y)), rstride=3, cstride=3, ... alpha=0.4, color='m', label='linear interp')
>>> # ground truth >>> ax.plot_wireframe(X, Y, ff(X, Y), rstride=3, cstride=3, ... alpha=0.4, label='ground truth') >>> plt.legend() >>> plt.show()
Other examples are given in the tutorial.
- Attributes:
- gridtuple of ndarrays
The points defining the regular grid in n dimensions. This tuple defines the full grid via
np.meshgrid(*grid, indexing='ij')- valuesndarray
Data values at the grid.
- methodstr
Interpolation method.
- fill_valuefloat or
None Use this value for out-of-bounds arguments to
__call__.- bounds_errorbool
If
True, out-of-bounds argument raise aValueError.
Methods
__call__(xi[, method, nu])Interpolation at coordinates.