dunnett#
- scipy.stats.dunnett(*samples, control, alternative='two-sided', random_state=None)[source]#
Dunnett’s test: multiple comparisons of means against a control group.
This is an implementation of Dunnett’s original, single-step test as described in [1].
- Parameters:
- sample1, sample2, …1D array_like
The sample measurements for each experimental group.
- control1D array_like
The sample measurements for the control group.
- alternative{‘two-sided’, ‘less’, ‘greater’}, optional
Defines the alternative hypothesis.
The null hypothesis is that the means of the distributions underlying the samples and control are equal. The following alternative hypotheses are available (default is ‘two-sided’):
‘two-sided’: the means of the distributions underlying the samples and control are unequal.
‘less’: the means of the distributions underlying the samples are less than the mean of the distribution underlying the control.
‘greater’: the means of the distributions underlying the samples are greater than the mean of the distribution underlying the control.
- random_state{None, int,
numpy.random.Generator}, optional If random_state is an int or None, a new
numpy.random.Generatoris created usingnp.random.default_rng(random_state). If random_state is already aGeneratorinstance, then the provided instance is used.The random number generator is used to control the randomized Quasi-Monte Carlo integration of the multivariate-t distribution.
- Returns:
- res
DunnettResult An object containing attributes:
- statisticfloat ndarray
The computed statistic of the test for each comparison. The element at index
iis the statistic for the comparison between groupsiand the control.- pvaluefloat ndarray
The computed p-value of the test for each comparison. The element at index
iis the p-value for the comparison between groupiand the control.
And the following method:
- confidence_interval(confidence_level=0.95) :
Compute the difference in means of the groups with the control +- the allowance.
- res
See also
tukey_hsdperforms pairwise comparison of means.
Notes
Like the independent-sample t-test, Dunnett’s test [1] is used to make inferences about the means of distributions from which samples were drawn. However, when multiple t-tests are performed at a fixed significance level, the “family-wise error rate” - the probability of incorrectly rejecting the null hypothesis in at least one test - will exceed the significance level. Dunnett’s test is designed to perform multiple comparisons while controlling the family-wise error rate.
Dunnett’s test compares the means of multiple experimental groups against a single control group. Tukey’s Honestly Significant Difference Test is another multiple-comparison test that controls the family-wise error rate, but
tukey_hsdperforms all pairwise comparisons between groups. When pairwise comparisons between experimental groups are not needed, Dunnett’s test is preferable due to its higher power.The use of this test relies on several assumptions.
The observations are independent within and among groups.
The observations within each group are normally distributed.
The distributions from which the samples are drawn have the same finite variance.
References
[1] (1,2,3)Charles W. Dunnett. “A Multiple Comparison Procedure for Comparing Several Treatments with a Control.” Journal of the American Statistical Association, 50:272, 1096-1121, DOI:10.1080/01621459.1955.10501294, 1955.
Examples
In [1], the influence of drugs on blood count measurements on three groups of animal is investigated.
The following table summarizes the results of the experiment in which two groups received different drugs, and one group acted as a control. Blood counts (in millions of cells per cubic millimeter) were recorded:
>>> import numpy as np >>> control = np.array([7.40, 8.50, 7.20, 8.24, 9.84, 8.32]) >>> drug_a = np.array([9.76, 8.80, 7.68, 9.36]) >>> drug_b = np.array([12.80, 9.68, 12.16, 9.20, 10.55])
We would like to see if the means between any of the groups are significantly different. First, visually examine a box and whisker plot.
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) >>> ax.boxplot([control, drug_a, drug_b]) >>> ax.set_xticklabels(["Control", "Drug A", "Drug B"]) >>> ax.set_ylabel("mean") >>> plt.show()
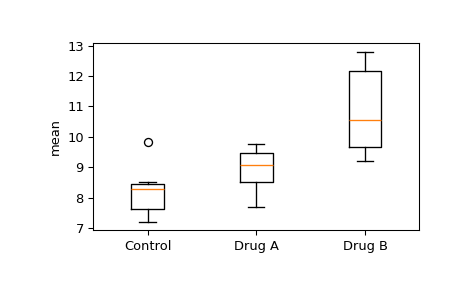
Note the overlapping interquartile ranges of the drug A group and control group and the apparent separation between the drug B group and control group.
Next, we will use Dunnett’s test to assess whether the difference between group means is significant while controlling the family-wise error rate: the probability of making any false discoveries. Let the null hypothesis be that the experimental groups have the same mean as the control and the alternative be that an experimental group does not have the same mean as the control. We will consider a 5% family-wise error rate to be acceptable, and therefore we choose 0.05 as the threshold for significance.
>>> from scipy.stats import dunnett >>> res = dunnett(drug_a, drug_b, control=control) >>> res.pvalue array([0.62004941, 0.0059035 ]) # may vary
The p-value corresponding with the comparison between group A and control exceeds 0.05, so we do not reject the null hypothesis for that comparison. However, the p-value corresponding with the comparison between group B and control is less than 0.05, so we consider the experimental results to be evidence against the null hypothesis in favor of the alternative: group B has a different mean than the control group.