scipy.signal.spectrogram

scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, mode='psd')

Compute a spectrogram with consecutive Fourier transforms (legacy function).

Spectrograms can be used as a way of visualizing the change of a nonstationary signal’s frequency content over time.

Legacy

This function is considered legacy and will no longer receive updates. This could also mean it will be removed in future SciPy versions. ShortTimeFFT is a newer STFT / ISTFT implementation with more features also including a spectrogram method. A comparison between the implementations can be found in the Short-Time Fourier Transform section of the SciPy User Guide.

Parameters:

xarray_like

Time series of measurement values

fsfloat, optional

Sampling frequency of the x time series. Defaults to 1.0.

windowstr or tuple or array_like, optional

Desired window to use. If window is a string or tuple, it is passed to get_window to generate the window values, which are DFT-even by default. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a Tukey window with shape parameter of 0.25.

npersegint, optional

Length of each segment. Defaults to None, but if window is str or tuple, is set to 256, and if window is array_like, is set to the length of the window.

noverlapint, optional

Number of points to overlap between segments. If None, noverlap = nperseg // 8. Defaults to None.

nfftint, optional

Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.

detrendstr or function or False, optional

Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to the detrend function. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to ‘constant’.

return_onesidedbool, optional

If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Defaults to True, but for complex data, a two-sided spectrum is always returned.

scaling{ ‘density’, ‘spectrum’ }, optional

Selects between computing the power spectral density (‘density’) where Sxx has units of V**2/Hz and computing the power spectrum (‘spectrum’) where Sxx has units of V**2, if x is measured in V and fs is measured in Hz. Defaults to ‘density’.

axisint, optional

Axis along which the spectrogram is computed; the default is over the last axis (i.e. axis=-1).

modestr, optional

Defines what kind of return values are expected. Options are [‘psd’, ‘complex’, ‘magnitude’, ‘angle’, ‘phase’]. ‘complex’ is equivalent to the output of stft with no padding or boundary extension. ‘magnitude’ returns the absolute magnitude of the STFT. ‘angle’ and ‘phase’ return the complex angle of the STFT, with and without unwrapping, respectively.

Returns:

fndarray

Array of sample frequencies.

tndarray

Array of segment times.

Sxxndarray

Spectrogram of x. By default, the last axis of Sxx corresponds to the segment times.

See also

periodogram

Simple, optionally modified periodogram

lombscargle

Lomb-Scargle periodogram for unevenly sampled data

welch

Power spectral density by Welch’s method.

csd

Cross spectral density by Welch’s method.

ShortTimeFFT

Newer STFT/ISTFT implementation providing more features, which also includes a spectrogram method.

Notes

An appropriate amount of overlap will depend on the choice of window and on your requirements. In contrast to welch’s method, where the entire data stream is averaged over, one may wish to use a smaller overlap (or perhaps none at all) when computing a spectrogram, to maintain some statistical independence between individual segments. It is for this reason that the default window is a Tukey window with 1/8th of a window’s length overlap at each end.

Added in version 0.16.0.

References

[1]

Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time Signal Processing”, Prentice Hall, 1999.

Examples

Try it in your browser!

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fftshift
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Generate a test signal, a 2 Vrms sine wave whose frequency is slowly modulated around 3kHz, corrupted by white noise of exponentially decreasing magnitude sampled at 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

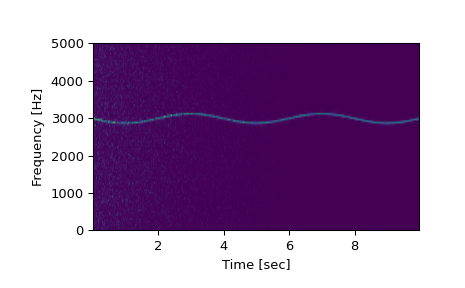
Compute and plot the spectrogram.

>>> f, t, Sxx = signal.spectrogram(x, fs)
>>> plt.pcolormesh(t, f, Sxx, shading='gouraud')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

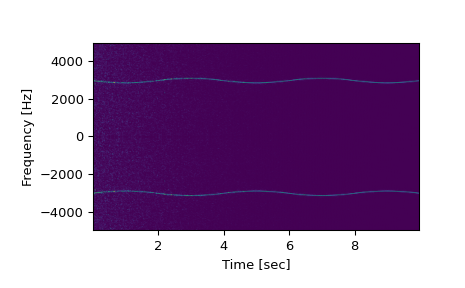
Note, if using output that is not one sided, then use the following:

>>> f, t, Sxx = signal.spectrogram(x, fs, return_onesided=False)
>>> plt.pcolormesh(t, fftshift(f), fftshift(Sxx, axes=0), shading='gouraud')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

Go BackOpen In Tab