scipy.signal.max_len_seq#

scipy.signal.max_len_seq(nbits, state=None, length=None, taps=None)[source]#

Maximum length sequence (MLS) generator.

Parameters:

nbitsint: Number of bits to use. Length of the resulting sequence will be (2**nbits) - 1. Note that generating long sequences (e.g., greater than nbits == 16) can take a long time.
statearray_like, optional: If array, must be of length nbits, and will be cast to binary (bool) representation. If None, a seed of ones will be used, producing a repeatable representation. If state is all zeros, an error is raised as this is invalid. Default: None.
lengthint, optional: Number of samples to compute. If None, the entire length (2**nbits) - 1 is computed.
tapsarray_like, optional: Polynomial taps to use (e.g., [7, 6, 1] for an 8-bit sequence). If None, taps will be automatically selected (for up to nbits == 32).

Returns:

seqarray: Resulting MLS sequence of 0’s and 1’s.
statearray: The final state of the shift register.

Notes

The algorithm for MLS generation is generically described in:

https://en.wikipedia.org/wiki/Maximum_length_sequence

The default values for taps are specifically taken from the first option listed for each value of nbits in:

https://web.archive.org/web/20181001062252/http://www.newwaveinstruments.com/resources/articles/m_sequence_linear_feedback_shift_register_lfsr.htm

Added in version 0.15.0.

Examples

MLS uses binary convention:

>>> from scipy.signal import max_len_seq
>>> max_len_seq(4)[0]
array([1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int8)

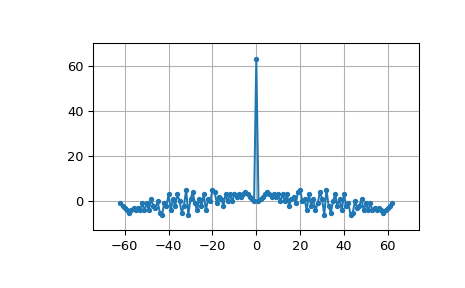
MLS has a white spectrum (except for DC):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1  # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
>>> plt.plot(fftshift(fftfreq(N)), fftshift(np.abs(spec)), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

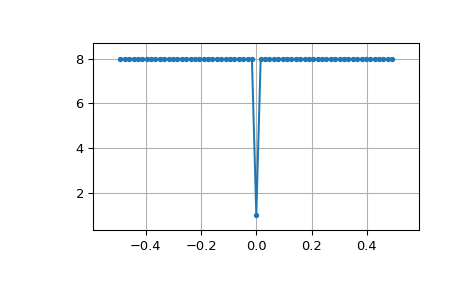
../../_images/scipy-signal-max_len_seq-1_00_00.png

Circular autocorrelation of MLS is an impulse:

>>> acorrcirc = ifft(spec * np.conj(spec)).real
>>> plt.figure()
>>> plt.plot(np.arange(-N/2+1, N/2+1), fftshift(acorrcirc), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

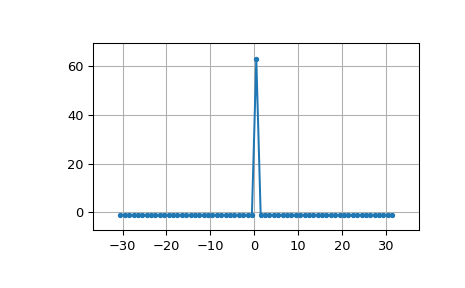
../../_images/scipy-signal-max_len_seq-1_01_00.png

Linear autocorrelation of MLS is approximately an impulse:

>>> acorr = np.correlate(seq, seq, 'full')
>>> plt.figure()
>>> plt.plot(np.arange(-N+1, N), acorr, '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-max_len_seq-1_02_00.png