scipy.interpolate.SmoothSphereBivariateSpline

class scipy.interpolate.SmoothSphereBivariateSpline(theta, phi, r, w=None, s=0.0, eps=1e-16)

Smooth bivariate spline approximation in spherical coordinates.

Added in version 0.11.0.

Parameters:

theta, phi, rarray_like

1-D sequences of data points (order is not important). Coordinates must be given in radians. Theta must lie within the interval [0, pi], and phi must lie within the interval [0, 2pi].

warray_like, optional

Positive 1-D sequence of weights.

sfloat, optional

Positive smoothing factor defined for estimation condition: sum((w(i)*(r(i) - s(theta(i), phi(i))))**2, axis=0) <= s Default s=len(w) which should be a good value if 1/w[i] is an estimate of the standard deviation of r[i].

epsfloat, optional

A threshold for determining the effective rank of an over-determined linear system of equations. eps should have a value within the open interval (0, 1), the default is 1e-16.

See also

BivariateSpline

a base class for bivariate splines.

UnivariateSpline

a smooth univariate spline to fit a given set of data points.

SmoothBivariateSpline

a smoothing bivariate spline through the given points

LSQBivariateSpline

a bivariate spline using weighted least-squares fitting

RectSphereBivariateSpline

a bivariate spline over a rectangular mesh on a sphere

LSQSphereBivariateSpline

a bivariate spline in spherical coordinates using weighted least-squares fitting

RectBivariateSpline

a bivariate spline over a rectangular mesh.

bisplrep

a function to find a bivariate B-spline representation of a surface

bisplev

a function to evaluate a bivariate B-spline and its derivatives

Notes

For more information, see the FITPACK site about this function.

Examples

Try it in your browser!

Suppose we have global data on a coarse grid (the input data does not have to be on a grid):

>>> import numpy as np
>>> theta = np.linspace(0., np.pi, 7)
>>> phi = np.linspace(0., 2*np.pi, 9)
>>> data = np.empty((theta.shape[0], phi.shape[0]))
>>> data[:,0], data[0,:], data[-1,:] = 0., 0., 0.
>>> data[1:-1,1], data[1:-1,-1] = 1., 1.
>>> data[1,1:-1], data[-2,1:-1] = 1., 1.
>>> data[2:-2,2], data[2:-2,-2] = 2., 2.
>>> data[2,2:-2], data[-3,2:-2] = 2., 2.
>>> data[3,3:-2] = 3.
>>> data = np.roll(data, 4, 1)

We need to set up the interpolator object

>>> lats, lons = np.meshgrid(theta, phi)
>>> from scipy.interpolate import SmoothSphereBivariateSpline
>>> lut = SmoothSphereBivariateSpline(lats.ravel(), lons.ravel(),
...                                   data.T.ravel(), s=3.5)

As a first test, we’ll see what the algorithm returns when run on the input coordinates

>>> data_orig = lut(theta, phi)

Finally we interpolate the data to a finer grid

>>> fine_lats = np.linspace(0., np.pi, 70)
>>> fine_lons = np.linspace(0., 2 * np.pi, 90)

>>> data_smth = lut(fine_lats, fine_lons)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(131)
>>> ax1.imshow(data, interpolation='nearest')
>>> ax2 = fig.add_subplot(132)
>>> ax2.imshow(data_orig, interpolation='nearest')
>>> ax3 = fig.add_subplot(133)
>>> ax3.imshow(data_smth, interpolation='nearest')
>>> plt.show()

Go BackOpen In Tab

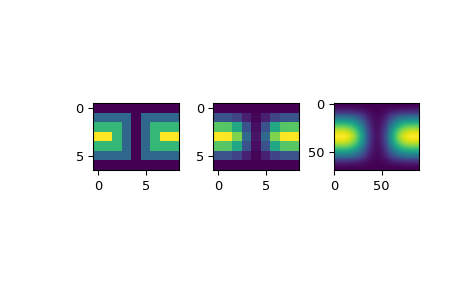
Methods

__call__(theta, phi[, dtheta, dphi, grid])	Evaluate the spline or its derivatives at given positions.
ev(theta, phi[, dtheta, dphi])	Evaluate the spline at points
get_coeffs()	Return spline coefficients.
get_knots()	Return a tuple (tx,ty) where tx,ty contain knots positions of the spline with respect to x-, y-variable, respectively.
get_residual()	Return weighted sum of squared residuals of the spline approximation: sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0)
partial_derivative(dx, dy)	Construct a new spline representing a partial derivative of this spline.