scipy.interpolate.Akima1DInterpolator#

class scipy.interpolate.Akima1DInterpolator(x, y, axis=0, *, method='akima')[source]#

Akima interpolator

Fit piecewise cubic polynomials, given vectors x and y. The interpolation method by Akima uses a continuously differentiable sub-spline built from piecewise cubic polynomials. The resultant curve passes through the given data points and will appear smooth and natural.

Parameters:

xndarray, shape (npoints, ): 1-D array of monotonically increasing real values.
yndarray, shape (…, npoints, …): N-D array of real values. The length of y along the interpolation axis must be equal to the length of x. Use the axis parameter to select the interpolation axis.

Deprecated since version 1.13.0: Complex data is deprecated and will raise an error in SciPy 1.15.0. If you are trying to use the real components of the passed array, use np.real on y.
axisint, optional: Axis in the y array corresponding to the x-coordinate values. Defaults to axis=0.
method{‘akima’, ‘makima’}, optional: If "makima", use the modified Akima interpolation [2]. Defaults to "akima", use the Akima interpolation [1].

Added in version 1.13.0.

See also

PchipInterpolator: PCHIP 1-D monotonic cubic interpolator.
CubicSpline: Cubic spline data interpolator.
PPoly: Piecewise polynomial in terms of coefficients and breakpoints

Notes

Added in version 0.14.

Use only for precise data, as the fitted curve passes through the given points exactly. This routine is useful for plotting a pleasingly smooth curve through a few given points for purposes of plotting.

Let \(\delta_i = (y_{i+1} - y_i) / (x_{i+1} - x_i)\) be the slopes of the interval \(\left[x_i, x_{i+1}\right)\). Akima’s derivative at \(x_i\) is defined as:

\[d_i = \frac{w_1}{w_1 + w_2}\delta_{i-1} + \frac{w_2}{w_1 + w_2}\delta_i\]

In the Akima interpolation [1] (method="akima"), the weights are:

\[\begin{split}\begin{aligned} w_1 &= |\delta_{i+1} - \delta_i| \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| \end{aligned}\end{split}\]

In the modified Akima interpolation [2] (method="makima"), to eliminate overshoot and avoid edge cases of both numerator and denominator being equal to 0, the weights are modified as follows:

\[\begin{split}\begin{align*} w_1 &= |\delta_{i+1} - \delta_i| + |\delta_{i+1} + \delta_i| / 2 \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| + |\delta_{i-1} + \delta_{i-2}| / 2 \end{align*}\end{split}\]

References

[1] (1,2)

A new method of interpolation and smooth curve fitting based on local procedures. Hiroshi Akima, J. ACM, October 1970, 17(4), 589-602. DOI:10.1145/321607.321609

[2] (1,2)

Makima Piecewise Cubic Interpolation. Cleve Moler and Cosmin Ionita, 2019. https://blogs.mathworks.com/cleve/2019/04/29/makima-piecewise-cubic-interpolation/

Examples

Comparison of method="akima" and method="makima":

>>> import numpy as np
>>> from scipy.interpolate import Akima1DInterpolator
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(1, 7, 7)
>>> y = np.array([-1, -1, -1, 0, 1, 1, 1])
>>> xs = np.linspace(min(x), max(x), num=100)
>>> y_akima = Akima1DInterpolator(x, y, method="akima")(xs)
>>> y_makima = Akima1DInterpolator(x, y, method="makima")(xs)

>>> fig, ax = plt.subplots()
>>> ax.plot(x, y, "o", label="data")
>>> ax.plot(xs, y_akima, label="akima")
>>> ax.plot(xs, y_makima, label="makima")
>>> ax.legend()
>>> fig.show()

The overshoot that occured in "akima" has been avoided in "makima".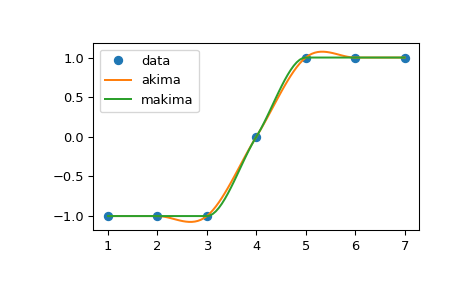

../../_images/scipy-interpolate-Akima1DInterpolator-1.png

Attributes:

axis
c
extrapolate
x

Methods

`__call__`(x[, nu, extrapolate])	Evaluate the piecewise polynomial or its derivative.
`derivative`([nu])	Construct a new piecewise polynomial representing the derivative.
`antiderivative`([nu])	Construct a new piecewise polynomial representing the antiderivative.
`roots`([discontinuity, extrapolate])	Find real roots of the piecewise polynomial.