scipy.stats.vonmises

scipy.stats.vonmises = <scipy.stats._continuous_distns.vonmises_gen object>

A Von Mises continuous random variable.

As an instance of the rv_continuous class, vonmises object inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.

See also

scipy.stats.vonmises_fisher

Von-Mises Fisher distribution on a hypersphere

Notes

The probability density function for vonmises and vonmises_line is:

\[f(x, \kappa) = \frac{ \exp(\kappa \cos(x)) }{ 2 \pi I_0(\kappa) }\]

for \(-\pi \le x \le \pi\), \(\kappa > 0\). \(I_0\) is the modified Bessel function of order zero (scipy.special.i0).

vonmises is a circular distribution which does not restrict the distribution to a fixed interval. Currently, there is no circular distribution framework in SciPy. The cdf is implemented such that cdf(x + 2*np.pi) == cdf(x) + 1.

vonmises_line is the same distribution, defined on \([-\pi, \pi]\) on the real line. This is a regular (i.e. non-circular) distribution.

Note about distribution parameters: vonmises and vonmises_line take kappa as a shape parameter (concentration) and loc as the location (circular mean). A scale parameter is accepted but does not have any effect.

Examples

Import the necessary modules.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import vonmises

Define distribution parameters.

>>> loc = 0.5 * np.pi  # circular mean
>>> kappa = 1  # concentration

Compute the probability density at x=0 via the pdf method.

>>> vonmises.pdf(loc, kappa, 0)
0.12570826359722018

Verify that the percentile function ppf inverts the cumulative distribution function cdf up to floating point accuracy.

>>> x = 1
>>> cdf_value = vonmises.cdf(loc=loc, kappa=kappa, x=x)
>>> ppf_value = vonmises.ppf(cdf_value, loc=loc, kappa=kappa)
>>> x, cdf_value, ppf_value
(1, 0.31489339900904967, 1.0000000000000004)

Draw 1000 random variates by calling the rvs method.

>>> number_of_samples = 1000
>>> samples = vonmises(loc=loc, kappa=kappa).rvs(number_of_samples)

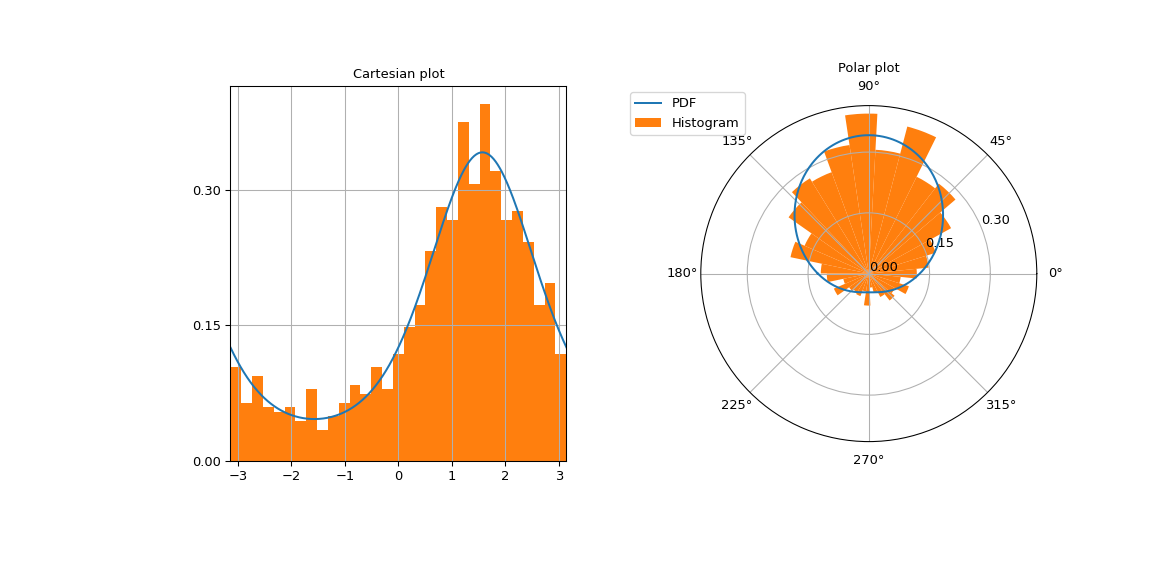
Plot the von Mises density on a Cartesian and polar grid to emphasize that is is a circular distribution.

>>> fig = plt.figure(figsize=(12, 6))
>>> left = plt.subplot(121)
>>> right = plt.subplot(122, projection='polar')
>>> x = np.linspace(-np.pi, np.pi, 500)
>>> vonmises_pdf = vonmises.pdf(loc, kappa, x)
>>> ticks = [0, 0.15, 0.3]

The left image contains the Cartesian plot.

>>> left.plot(x, vonmises_pdf)
>>> left.set_yticks(ticks)
>>> number_of_bins = int(np.sqrt(number_of_samples))
>>> left.hist(samples, density=True, bins=number_of_bins)
>>> left.set_title("Cartesian plot")
>>> left.set_xlim(-np.pi, np.pi)
>>> left.grid(True)

The right image contains the polar plot.

>>> right.plot(x, vonmises_pdf, label="PDF")
>>> right.set_yticks(ticks)
>>> right.hist(samples, density=True, bins=number_of_bins,
...            label="Histogram")
>>> right.set_title("Polar plot")
>>> right.legend(bbox_to_anchor=(0.15, 1.06))

Methods

rvs(kappa, loc=0, scale=1, size=1, random_state=None)	Random variates.
pdf(x, kappa, loc=0, scale=1)	Probability density function.
logpdf(x, kappa, loc=0, scale=1)	Log of the probability density function.
cdf(x, kappa, loc=0, scale=1)	Cumulative distribution function.
logcdf(x, kappa, loc=0, scale=1)	Log of the cumulative distribution function.
sf(x, kappa, loc=0, scale=1)	Survival function (also defined as 1 - cdf, but sf is sometimes more accurate).
logsf(x, kappa, loc=0, scale=1)	Log of the survival function.
ppf(q, kappa, loc=0, scale=1)	Percent point function (inverse of cdf — percentiles).
isf(q, kappa, loc=0, scale=1)	Inverse survival function (inverse of sf).
moment(order, kappa, loc=0, scale=1)	Non-central moment of the specified order.
stats(kappa, loc=0, scale=1, moments=’mv’)	Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(kappa, loc=0, scale=1)	(Differential) entropy of the RV.
fit(data)	Parameter estimates for generic data. See scipy.stats.rv_continuous.fit for detailed documentation of the keyword arguments.
expect(func, args=(kappa,), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Expected value of a function (of one argument) with respect to the distribution.
median(kappa, loc=0, scale=1)	Median of the distribution.
mean(kappa, loc=0, scale=1)	Mean of the distribution.
var(kappa, loc=0, scale=1)	Variance of the distribution.
std(kappa, loc=0, scale=1)	Standard deviation of the distribution.
interval(confidence, kappa, loc=0, scale=1)	Confidence interval with equal areas around the median.