scipy.signal.butter

scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba', fs=None)

Butterworth digital and analog filter design.

Design an Nth-order digital or analog Butterworth filter and return the filter coefficients.

Parameters:

Nint

The order of the filter. For ‘bandpass’ and ‘bandstop’ filters, the resulting order of the final second-order sections (‘sos’) matrix is 2*N, with N the number of biquad sections of the desired system.

Wnarray_like

The critical frequency or frequencies. For lowpass and highpass filters, Wn is a scalar; for bandpass and bandstop filters, Wn is a length-2 sequence.

For a Butterworth filter, this is the point at which the gain drops to 1/sqrt(2) that of the passband (the “-3 dB point”).

For digital filters, if fs is not specified, Wn units are normalized from 0 to 1, where 1 is the Nyquist frequency (Wn is thus in half cycles / sample and defined as 2*critical frequencies / fs). If fs is specified, Wn is in the same units as fs.

For analog filters, Wn is an angular frequency (e.g. rad/s).

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional

The type of filter. Default is ‘lowpass’.

analogbool, optional

When True, return an analog filter, otherwise a digital filter is returned.

output{‘ba’, ‘zpk’, ‘sos’}, optional

Type of output: numerator/denominator (‘ba’), pole-zero (‘zpk’), or second-order sections (‘sos’). Default is ‘ba’ for backwards compatibility, but ‘sos’ should be used for general-purpose filtering.

fsfloat, optional

The sampling frequency of the digital system.

New in version 1.2.0.

Returns:

b, andarray, ndarray

Numerator (b) and denominator (a) polynomials of the IIR filter. Only returned if output='ba'.

z, p, kndarray, ndarray, float

Zeros, poles, and system gain of the IIR filter transfer function. Only returned if output='zpk'.

sosndarray

Second-order sections representation of the IIR filter. Only returned if output='sos'.

See also

buttord, buttap

Notes

The Butterworth filter has maximally flat frequency response in the passband.

The 'sos' output parameter was added in 0.16.0.

If the transfer function form [b, a] is requested, numerical problems can occur since the conversion between roots and the polynomial coefficients is a numerically sensitive operation, even for N >= 4. It is recommended to work with the SOS representation.

Examples

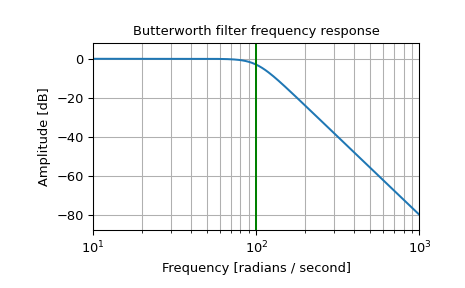
Design an analog filter and plot its frequency response, showing the critical points:

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Butterworth filter frequency response')
>>> plt.xlabel('Frequency [radians / second]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.show()

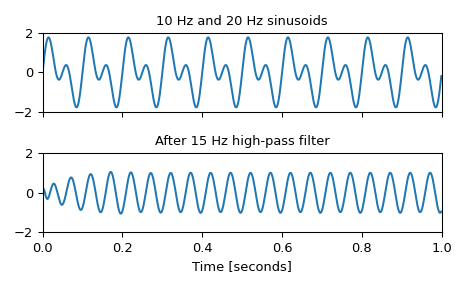
Generate a signal made up of 10 Hz and 20 Hz, sampled at 1 kHz

>>> t = np.linspace(0, 1, 1000, False)  # 1 second
>>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
>>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
>>> ax1.plot(t, sig)
>>> ax1.set_title('10 Hz and 20 Hz sinusoids')
>>> ax1.axis([0, 1, -2, 2])

Design a digital high-pass filter at 15 Hz to remove the 10 Hz tone, and apply it to the signal. (It’s recommended to use second-order sections format when filtering, to avoid numerical error with transfer function (ba) format):

>>> sos = signal.butter(10, 15, 'hp', fs=1000, output='sos')
>>> filtered = signal.sosfilt(sos, sig)
>>> ax2.plot(t, filtered)
>>> ax2.set_title('After 15 Hz high-pass filter')
>>> ax2.axis([0, 1, -2, 2])
>>> ax2.set_xlabel('Time [seconds]')
>>> plt.tight_layout()
>>> plt.show()