scipy.interpolate.lagrange

scipy.interpolate.lagrange(x, w)

Return a Lagrange interpolating polynomial.

Given two 1-D arrays x and w, returns the Lagrange interpolating polynomial through the points (x, w).

Warning: This implementation is numerically unstable. Do not expect to be able to use more than about 20 points even if they are chosen optimally.

Parameters:

xarray_like

x represents the x-coordinates of a set of datapoints.

warray_like

w represents the y-coordinates of a set of datapoints, i.e., f(x).

Returns:

lagrangenumpy.poly1d instance

The Lagrange interpolating polynomial.

Examples

Interpolate \(f(x) = x^3\) by 3 points.

>>> import numpy as np
>>> from scipy.interpolate import lagrange
>>> x = np.array([0, 1, 2])
>>> y = x**3
>>> poly = lagrange(x, y)

Since there are only 3 points, Lagrange polynomial has degree 2. Explicitly, it is given by

\[\begin{split}\begin{aligned} L(x) &= 1\times \frac{x (x - 2)}{-1} + 8\times \frac{x (x-1)}{2} \\ &= x (-2 + 3x) \end{aligned}\end{split}\]

>>> from numpy.polynomial.polynomial import Polynomial
>>> Polynomial(poly.coef[::-1]).coef
array([ 0., -2.,  3.])

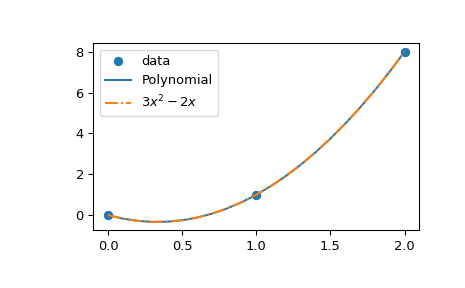
>>> import matplotlib.pyplot as plt
>>> x_new = np.arange(0, 2.1, 0.1)
>>> plt.scatter(x, y, label='data')
>>> plt.plot(x_new, Polynomial(poly.coef[::-1])(x_new), label='Polynomial')
>>> plt.plot(x_new, 3*x_new**2 - 2*x_new + 0*x_new,
...          label=r"$3 x^2 - 2 x$", linestyle='-.')
>>> plt.legend()
>>> plt.show()