scipy.interpolate.interp2d

class scipy.interpolate.interp2d(x, y, z, kind='linear', copy=True, bounds_error=False, fill_value=None)

Deprecated since version 1.10.0: interp2d is deprecated in SciPy 1.10 and will be removed in SciPy 1.12.0.

For legacy code, nearly bug-for-bug compatible replacements are RectBivariateSpline on regular grids, and bisplrep/bisplev for scattered 2D data.

In new code, for regular grids use RegularGridInterpolator instead. For scattered data, prefer LinearNDInterpolator or CloughTocher2DInterpolator.

For more details see https://gist.github.com/ev-br/8544371b40f414b7eaf3fe6217209bff

Interpolate over a 2-D grid.

x, y and z are arrays of values used to approximate some function f: z = f(x, y) which returns a scalar value z. This class returns a function whose call method uses spline interpolation to find the value of new points.

If x and y represent a regular grid, consider using RectBivariateSpline.

If z is a vector value, consider using interpn.

Note that calling interp2d with NaNs present in input values, or with decreasing values in x an y results in undefined behaviour.

Parameters:

x, yarray_like

Arrays defining the data point coordinates. The data point coordinates need to be sorted by increasing order.

If the points lie on a regular grid, x can specify the column coordinates and y the row coordinates, for example:

>>> x = [0,1,2];  y = [0,3]; z = [[1,2,3], [4,5,6]]

Otherwise, x and y must specify the full coordinates for each point, for example:

>>> x = [0,1,2,0,1,2];  y = [0,0,0,3,3,3]; z = [1,4,2,5,3,6]

If x and y are multidimensional, they are flattened before use.

zarray_like

The values of the function to interpolate at the data points. If z is a multidimensional array, it is flattened before use assuming Fortran-ordering (order=’F’). The length of a flattened z array is either len(x)*len(y) if x and y specify the column and row coordinates or len(z) == len(x) == len(y) if x and y specify coordinates for each point.

kind{‘linear’, ‘cubic’, ‘quintic’}, optional

The kind of spline interpolation to use. Default is ‘linear’.

copybool, optional

If True, the class makes internal copies of x, y and z. If False, references may be used. The default is to copy.

bounds_errorbool, optional

If True, when interpolated values are requested outside of the domain of the input data (x,y), a ValueError is raised. If False, then fill_value is used.

fill_valuenumber, optional

If provided, the value to use for points outside of the interpolation domain. If omitted (None), values outside the domain are extrapolated via nearest-neighbor extrapolation.

See also

RectBivariateSpline

Much faster 2-D interpolation if your input data is on a grid

bisplrep, bisplev

Spline interpolation based on FITPACK

BivariateSpline

a more recent wrapper of the FITPACK routines

interp1d

1-D version of this function

RegularGridInterpolator

interpolation on a regular or rectilinear grid in arbitrary dimensions.

interpn

Multidimensional interpolation on regular grids (wraps RegularGridInterpolator and RectBivariateSpline).

Notes

The minimum number of data points required along the interpolation axis is (k+1)**2, with k=1 for linear, k=3 for cubic and k=5 for quintic interpolation.

The interpolator is constructed by bisplrep, with a smoothing factor of 0. If more control over smoothing is needed, bisplrep should be used directly.

The coordinates of the data points to interpolate xnew and ynew have to be sorted by ascending order. interp2d is legacy and is not recommended for use in new code. New code should use RegularGridInterpolator instead.

Examples

Construct a 2-D grid and interpolate on it:

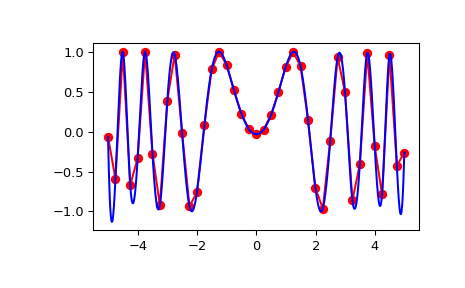
>>> import numpy as np
>>> from scipy import interpolate
>>> x = np.arange(-5.01, 5.01, 0.25)
>>> y = np.arange(-5.01, 5.01, 0.25)
>>> xx, yy = np.meshgrid(x, y)
>>> z = np.sin(xx**2+yy**2)
>>> f = interpolate.interp2d(x, y, z, kind='cubic')

Now use the obtained interpolation function and plot the result:

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(-5.01, 5.01, 1e-2)
>>> ynew = np.arange(-5.01, 5.01, 1e-2)
>>> znew = f(xnew, ynew)
>>> plt.plot(x, z[0, :], 'ro-', xnew, znew[0, :], 'b-')
>>> plt.show()

Methods

__call__(x, y[, dx, dy, assume_sorted])

interp2d is deprecated! interp2d is deprecated in SciPy 1.10 and will be removed in SciPy 1.12.0.