scipy.signal.iirpeak

scipy.signal.iirpeak(w0, Q)

Design second-order IIR peak (resonant) digital filter.

A peak filter is a band-pass filter with a narrow bandwidth (high quality factor). It rejects components outside a narrow frequency band.

Parameters:

w0 : float

Normalized frequency to be retained in a signal. It is a scalar that must satisfy 0 < w0 < 1, with w0 = 1 corresponding to half of the sampling frequency.

Q : float

Quality factor. Dimensionless parameter that characterizes peak filter -3 dB bandwidth bw relative to its center frequency, Q = w0/bw.

Returns:

b, a : ndarray, ndarray

Numerator (b) and denominator (a) polynomials of the IIR filter.

See also

iirnotch

Notes

New in version 0.19.0.

References

[1]	Sophocles J. Orfanidis, “Introduction To Signal Processing”, Prentice-Hall, 1996

Examples

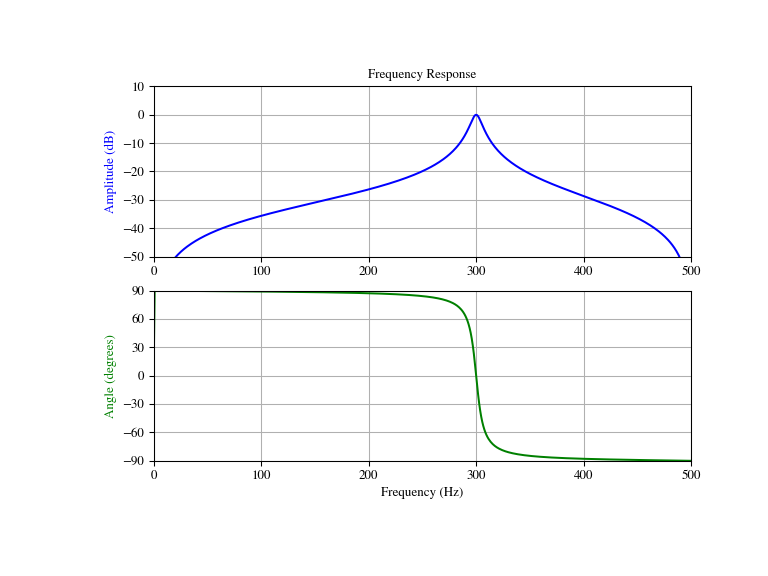
Design and plot filter to remove the frequencies other than the 300Hz component from a signal sampled at 1000Hz, using a quality factor Q = 30

>>> from scipy import signal
>>> import numpy as np
>>> import matplotlib.pyplot as plt

>>> fs = 1000.0  # Sample frequency (Hz)
>>> f0 = 300.0  # Frequency to be retained (Hz)
>>> Q = 30.0  # Quality factor
>>> w0 = f0/(fs/2)  # Normalized Frequency
>>> # Design peak filter
>>> b, a = signal.iirpeak(w0, Q)

>>> # Frequency response
>>> w, h = signal.freqz(b, a)
>>> # Generate frequency axis
>>> freq = w*fs/(2*np.pi)
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6))
>>> ax[0].plot(freq, 20*np.log10(abs(h)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude (dB)", color='blue')
>>> ax[0].set_xlim([0, 500])
>>> ax[0].set_ylim([-50, 10])
>>> ax[0].grid()
>>> ax[1].plot(freq, np.unwrap(np.angle(h))*180/np.pi, color='green')
>>> ax[1].set_ylabel("Angle (degrees)", color='green')
>>> ax[1].set_xlabel("Frequency (Hz)")
>>> ax[1].set_xlim([0, 500])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid()
>>> plt.show()