scipy.spatial.HalfspaceIntersection

class scipy.spatial.HalfspaceIntersection(halfspaces, interior_point, incremental=False, qhull_options=None)

Halfspace intersections in N dimensions.

New in version 0.19.0.

Parameters:

halfspaces : ndarray of floats, shape (nineq, ndim+1)

Stacked Inequalities of the form Ax + b <= 0 in format [A; b]

interior_point : ndarray of floats, shape (ndim,)

Point clearly inside the region defined by halfspaces. Also called a feasible point, it can be obtained by linear programming.

incremental : bool, optional

Allow adding new halfspaces incrementally. This takes up some additional resources.

qhull_options : str, optional

Additional options to pass to Qhull. See Qhull manual for details. (Default: “Qx” for ndim > 4 and “” otherwise) Option “H” is always enabled.

Raises:

QhullError

Raised when Qhull encounters an error condition, such as geometrical degeneracy when options to resolve are not enabled.

ValueError

Raised if an incompatible array is given as input.

Notes

The intersections are computed using the Qhull library. This reproduces the “qhalf” functionality of Qhull.

References

[Qhull]

http://www.qhull.org/

[R395]

(1, 2) S. Boyd, L. Vandenberghe, Convex Optimization, available at http://stanford.edu/~boyd/cvxbook/

Examples

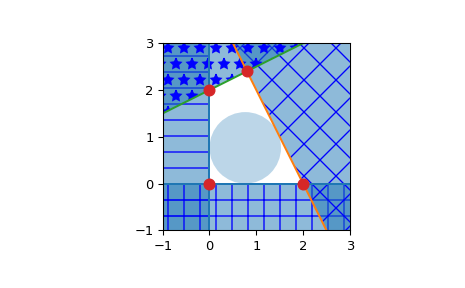
Halfspace intersection of planes forming some polygon

>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

Plot halfspaces as filled regions and intersection points:

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot('111', aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

By default, qhull does not provide with a way to compute an interior point. This can easily be computed using linear programming. Considering halfspaces of the form \(Ax + b \leq 0\), solving the linear program:

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

With \(A_i\) being the rows of A, i.e. the normals to each plane.

Will yield a point x that is furthest inside the convex polyhedron. To be precise, it is the center of the largest hypersphere of radius y inscribed in the polyhedron. This point is called the Chebyshev center of the polyhedron (see [R395] 4.3.1, pp148-149). The equations outputted by Qhull are always normalized.

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b)
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()

Attributes

halfspaces	(ndarray of double, shape (nineq, ndim+1)) Input halfspaces.
interior_point :ndarray of floats, shape (ndim,)	Input interior point.
intersections	(ndarray of double, shape (ninter, ndim)) Intersections of all halfspaces.
dual_points	(ndarray of double, shape (nineq, ndim)) Dual points of the input halfspaces.
dual_facets	(list of lists of ints) Indices of points forming the (non necessarily simplicial) facets of the dual convex hull.
dual_vertices	(ndarray of ints, shape (nvertices,)) Indices of halfspaces forming the vertices of the dual convex hull. For 2-D convex hulls, the vertices are in counterclockwise order. For other dimensions, they are in input order.
dual_equations	(ndarray of double, shape (nfacet, ndim+1)) [normal, offset] forming the hyperplane equation of the dual facet (see Qhull documentation for more).
dual_area	(float) Area of the dual convex hull
dual_volume	(float) Volume of the dual convex hull

Methods

add_halfspaces(halfspaces[, restart])	Process a set of additional new halfspaces.
close()	Finish incremental processing.