scipy.cluster.hierarchy.linkage¶
- scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean')¶
- Performs hierarchical/agglomerative clustering on the
condensed distance matrix y. y must be a
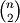 sized
vector where n is the number of original observations paired
in the distance matrix. The behavior of this function is very
similar to the MATLAB(TM) linkage function.
sized
vector where n is the number of original observations paired
in the distance matrix. The behavior of this function is very
similar to the MATLAB(TM) linkage function.A 4 by
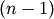 matrix Z is returned. At the
matrix Z is returned. At the
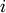 -th iteration, clusters with indices Z[i, 0] and
Z[i, 1] are combined to form cluster
-th iteration, clusters with indices Z[i, 0] and
Z[i, 1] are combined to form cluster 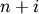 . A
cluster with an index less than
. A
cluster with an index less than 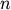 corresponds to one of
the
corresponds to one of
the 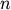 original observations. The distance between
clusters Z[i, 0] and Z[i, 1] is given by Z[i, 2]. The
fourth value Z[i, 3] represents the number of original
observations in the newly formed cluster.
original observations. The distance between
clusters Z[i, 0] and Z[i, 1] is given by Z[i, 2]. The
fourth value Z[i, 3] represents the number of original
observations in the newly formed cluster.The following linkage methods are used to compute the distance
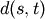 between two clusters
between two clusters 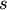 and
and
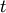 . The algorithm begins with a forest of clusters that
have yet to be used in the hierarchy being formed. When two
clusters
. The algorithm begins with a forest of clusters that
have yet to be used in the hierarchy being formed. When two
clusters 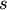 and
and 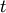 from this forest are combined
into a single cluster
from this forest are combined
into a single cluster 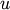 ,
, 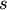 and
and 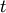 are
removed from the forest, and
are
removed from the forest, and 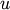 is added to the
forest. When only one cluster remains in the forest, the algorithm
stops, and this cluster becomes the root.
is added to the
forest. When only one cluster remains in the forest, the algorithm
stops, and this cluster becomes the root.A distance matrix is maintained at each iteration. The d[i,j] entry corresponds to the distance between cluster
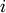 and
and
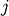 in the original forest.
in the original forest.At each iteration, the algorithm must update the distance matrix to reflect the distance of the newly formed cluster u with the remaining clusters in the forest.
Suppose there are
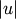 original observations
original observations
![u[0], \ldots, u[|u|-1]](../_images/math/fc6a7200130404042ef9469d1371adc30f4d4ffe.png) in cluster
in cluster 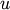 and
and
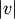 original objects
original objects ![v[0], \ldots, v[|v|-1]](../_images/math/d8148db3f0afe74312df26763af4382e5a52b1b8.png) in
cluster
in
cluster 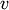 . Recall
. Recall 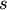 and
and 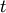 are
combined to form cluster
are
combined to form cluster 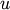 . Let
. Let 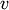 be any
remaining cluster in the forest that is not
be any
remaining cluster in the forest that is not 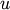 .
.The following are methods for calculating the distance between the newly formed cluster
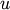 and each
and each 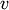 .
.method=’single’ assigns
![d(u,v) = \min(dist(u[i],v[j]))](../_images/math/5d7690bb05d67ea02e5015d79e500b80c40733a3.png)
for all points
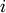 in cluster
in cluster 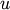 and
and
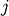 in cluster
in cluster 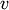 . This is also known as the
Nearest Point Algorithm.
. This is also known as the
Nearest Point Algorithm.method=’complete’ assigns
![d(u, v) = \max(dist(u[i],v[j]))](../_images/math/e8281806ed8c8d739e4317b09707c622d9d97635.png)
for all points
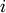 in cluster u and
in cluster u and 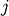 in
cluster
in
cluster 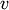 . This is also known by the Farthest Point
Algorithm or Voor Hees Algorithm.
. This is also known by the Farthest Point
Algorithm or Voor Hees Algorithm.method=’average’ assigns
![d(u,v) = \sum_{ij} \frac{d(u[i], v[j])}
{(|u|*|v|)}](../_images/math/453fb2bb40a60499bfd7c6c6aaf1086b73395ec1.png)
for all points
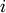 and
and 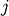 where
where 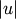 and
and 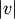 are the cardinalities of clusters
are the cardinalities of clusters 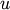 and
and 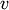 , respectively. This is also called the UPGMA
algorithm. This is called UPGMA.
, respectively. This is also called the UPGMA
algorithm. This is called UPGMA.method=’weighted’ assigns
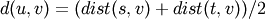
where cluster u was formed with cluster s and t and v is a remaining cluster in the forest. (also called WPGMA)
method=’centroid’ assigns
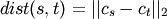
where
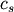 and
and 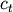 are the centroids of
clusters
are the centroids of
clusters 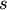 and
and 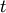 , respectively. When two
clusters
, respectively. When two
clusters 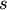 and
and 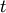 are combined into a new
cluster
are combined into a new
cluster 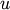 , the new centroid is computed over all the
original objects in clusters
, the new centroid is computed over all the
original objects in clusters 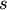 and
and 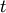 . The
distance then becomes the Euclidean distance between the
centroid of
. The
distance then becomes the Euclidean distance between the
centroid of 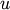 and the centroid of a remaining cluster
and the centroid of a remaining cluster
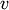 in the forest. This is also known as the UPGMC
algorithm.
in the forest. This is also known as the UPGMC
algorithm.method=’median’ assigns math:d(s,t) like the centroid method. When two clusters
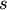 and
and 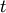 are combined
into a new cluster
are combined
into a new cluster 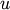 , the average of centroids s and t
give the new centroid
, the average of centroids s and t
give the new centroid 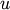 . This is also known as the
WPGMC algorithm.
. This is also known as the
WPGMC algorithm.method=’ward’ uses the Ward variance minimization algorithm. The new entry
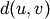 is computed as follows,
is computed as follows,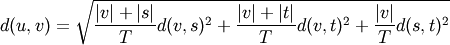
where
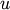 is the newly joined cluster consisting of
clusters
is the newly joined cluster consisting of
clusters 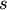 and
and 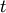 ,
, 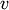 is an unused
cluster in the forest,
is an unused
cluster in the forest, 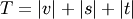 , and
, and
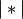 is the cardinality of its argument. This is also
known as the incremental algorithm.
is the cardinality of its argument. This is also
known as the incremental algorithm.
Warning: When the minimum distance pair in the forest is chosen, there may be two or more pairs with the same minimum distance. This implementation may chose a different minimum than the MATLAB(TM) version.
Parameters: - y : ndarray
A condensed or redundant distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of
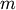 observation vectors in n dimensions may be passed as
an
observation vectors in n dimensions may be passed as
an 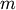 by
by 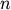 array.
array.
- method : string
The linkage algorithm to use. See the Linkage Methods section below for full descriptions.
- metric : string
The distance metric to use. See the distance.pdist function for a list of valid distance metrics.
Returns : - Z : ndarray
The hierarchical clustering encoded as a linkage matrix.
