Hierarchical clustering (scipy.cluster.hierarchy)¶
Warning
This documentation is work-in-progress and unorganized.
Function Reference¶
These functions cut hierarchical clusterings into flat clusterings or find the roots of the forest formed by a cut by providing the flat cluster ids of each observation.
| Function | Description |
| fcluster | forms flat clusters from hierarchical clusters. |
| fclusterdata | forms flat clusters directly from data. |
| leaders | singleton root nodes for flat cluster. |
These are routines for agglomerative clustering.
| Function | Description |
| linkage | agglomeratively clusters original observations. |
| single | the single/min/nearest algorithm. (alias) |
| complete | the complete/max/farthest algorithm. (alias) |
| average | the average/UPGMA algorithm. (alias) |
| weighted | the weighted/WPGMA algorithm. (alias) |
| centroid | the centroid/UPGMC algorithm. (alias) |
| median | the median/WPGMC algorithm. (alias) |
| ward | the Ward/incremental algorithm. (alias) |
These routines compute statistics on hierarchies.
| Function | Description |
| cophenet | computes the cophenetic distance between leaves. |
| from_mlab_linkage | converts a linkage produced by MATLAB(TM). |
| inconsistent | the inconsistency coefficients for cluster. |
| maxinconsts | the maximum inconsistency coefficient for each cluster. |
| maxdists | the maximum distance for each cluster. |
| maxRstat | the maximum specific statistic for each cluster. |
| to_mlab_linkage | converts a linkage to one MATLAB(TM) can understand. |
Routines for visualizing flat clusters.
| Function | Description |
| dendrogram | visualizes linkages (requires matplotlib). |
These are data structures and routines for representing hierarchies as tree objects.
| Function | Description |
| ClusterNode | represents cluster nodes in a cluster hierarchy. |
| leaves_list | a left-to-right traversal of the leaves. |
| to_tree | represents a linkage matrix as a tree object. |
These are predicates for checking the validity of linkage and inconsistency matrices as well as for checking isomorphism of two flat cluster assignments.
| Function | Description |
| is_valid_im | checks for a valid inconsistency matrix. |
| is_valid_linkage | checks for a valid hierarchical clustering. |
| is_isomorphic | checks if two flat clusterings are isomorphic. |
| is_monotonic | checks if a linkage is monotonic. |
| correspond | checks whether a condensed distance matrix corresponds with a linkage |
| num_obs_linkage | the number of observations corresponding to a linkage matrix. |
- MATLAB and MathWorks are registered trademarks of The MathWorks, Inc.
- Mathematica is a registered trademark of The Wolfram Research, Inc.
References¶
| [Sta07] | “Statistics toolbox.” API Reference Documentation. The MathWorks. http://www.mathworks.com/access/helpdesk/help/toolbox/stats/. Accessed October 1, 2007. |
| [Mti07] | “Hierarchical clustering.” API Reference Documentation. The Wolfram Research, Inc. http://reference.wolfram.com/mathematica/HierarchicalClustering/tutorial/HierarchicalClustering.html. Accessed October 1, 2007. |
| [Gow69] | Gower, JC and Ross, GJS. “Minimum Spanning Trees and Single Linkage Cluster Analysis.” Applied Statistics. 18(1): pp. 54–64. 1969. |
| [War63] | Ward Jr, JH. “Hierarchical grouping to optimize an objective function.” Journal of the American Statistical Association. 58(301): pp. 236–44. 1963. |
| [Joh66] | Johnson, SC. “Hierarchical clustering schemes.” Psychometrika. 32(2): pp. 241–54. 1966. |
| [Sne62] | Sneath, PH and Sokal, RR. “Numerical taxonomy.” Nature. 193: pp. 855–60. 1962. |
| [Bat95] | Batagelj, V. “Comparing resemblance measures.” Journal of Classification. 12: pp. 73–90. 1995. |
| [Sok58] | Sokal, RR and Michener, CD. “A statistical method for evaluating systematic relationships.” Scientific Bulletins. 38(22): pp. 1409–38. 1958. |
| [Ede79] | Edelbrock, C. “Mixture model tests of hierarchical clustering algorithms: the problem of classifying everybody.” Multivariate Behavioral Research. 14: pp. 367–84. 1979. |
| [Jai88] | Jain, A., and Dubes, R., “Algorithms for Clustering Data.” Prentice-Hall. Englewood Cliffs, NJ. 1988. |
| [Fis36] | Fisher, RA “The use of multiple measurements in taxonomic problems.” Annals of Eugenics, 7(2): 179-188. 1936 |
Copyright Notice¶
Copyright (C) Damian Eads, 2007-2008. New BSD License.
- class scipy.cluster.hierarchy.ClusterNode(id, left=None, right=None, dist=0, count=1)¶
A tree node class for representing a cluster. Leaf nodes correspond to original observations, while non-leaf nodes correspond to non-singleton clusters.
The to_tree function converts a matrix returned by the linkage function into an easy-to-use tree representation.
Seealso : - to_tree: for converting a linkage matrix Z into a tree object.
Methods
get_count get_id get_left get_right is_leaf pre_order - get_count()¶
The number of leaf nodes (original observations) belonging to the cluster node nd. If the target node is a leaf, 1 is returned.
Returns : - c : int
The number of leaf nodes below the target node.
- get_id()¶
The identifier of the target node. For
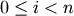 ,
,
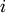 corresponds to original observation
corresponds to original observation
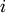 . For
. For 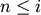 <
< 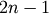 ,
,
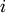 corresponds to non-singleton cluster formed at
iteration
corresponds to non-singleton cluster formed at
iteration 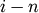 .
.Returns : - id : int
The identifier of the target node.
- get_left()¶
Returns a reference to the left child tree object. If the node is a leaf, None is returned.
Returns : - left : ClusterNode
The left child of the target node.
- get_right()¶
Returns a reference to the right child tree object. If the node is a leaf, None is returned.
Returns : - right : ClusterNode
The left child of the target node.
- is_leaf()¶
Returns True iff the target node is a leaf.
Returns : - leafness : bool
True if the target node is a leaf node.
- pre_order(func=<function <lambda> at 0x16327aa0>)¶
Performs preorder traversal without recursive function calls. When a leaf node is first encountered, func is called with the leaf node as its argument, and its result is appended to the list.
For example, the statement:
ids = root.pre_order(lambda x: x.id)
returns a list of the node ids corresponding to the leaf nodes of the tree as they appear from left to right.
Parameters : - func : function Applied to each leaf ClusterNode object in the pre-order traversal. Given the i’th leaf node in the pre-order traversal n[i], the result of func(n[i]) is stored in L[i]. If not provided, the index of the original observation to which the node corresponds is used.
Returns : - L : list The pre-order traversal.
- scipy.cluster.hierarchy.average(y)¶
Performs average/UPGMA linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Parameters : - y : ndarray
The upper triangular of the distance matrix. The result of pdist is returned in this form.
Returns : - Z : ndarray
A linkage matrix containing the hierarchical clustering. See the linkage function documentation for more information on its structure.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
- scipy.cluster.hierarchy.centroid(y)¶
Performs centroid/UPGMC linkage. See linkage for more information on the return structure and algorithm.
The following are common calling conventions:
Z = centroid(y)
Performs centroid/UPGMC linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Z = centroid(X)
Performs centroid/UPGMC linkage on the observation matrix X using Euclidean distance as the distance metric. See linkage for more information on the return structure and algorithm.
Parameters : - Q : ndarray
A condensed or redundant distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of m observation vectors in n dimensions may be passed as a m by n array.
Returns : - Z : ndarray
A linkage matrix containing the hierarchical clustering. See the linkage function documentation for more information on its structure.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
- scipy.cluster.hierarchy.complete(y)¶
Performs complete complete/max/farthest point linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Parameters : - y : ndarray
The upper triangular of the distance matrix. The result of pdist is returned in this form.
Returns : - Z : ndarray
A linkage matrix containing the hierarchical clustering. See the linkage function documentation for more information on its structure.
- scipy.cluster.hierarchy.cophenet(Z, Y=None)¶
Calculates the cophenetic distances between each observation in the hierarchical clustering defined by the linkage Z.
Suppose p and q are original observations in disjoint clusters s and t, respectively and s and t are joined by a direct parent cluster u. The cophenetic distance between observations i and j is simply the distance between clusters s and t.
Parameters : - Z : ndarray The hierarchical clustering encoded as an array (see linkage function).
- Y : ndarray (optional)
Calculates the cophenetic correlation coefficient c of a
hierarchical clustering defined by the linkage matrix Z
of a set of
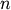 observations in
observations in 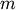 dimensions. Y is the condensed distance matrix from which
Z was generated.
dimensions. Y is the condensed distance matrix from which
Z was generated.
Returns : (c, {d}) - c : ndarray
The cophentic correlation distance (if y is passed).
- d : ndarray
The cophenetic distance matrix in condensed form. The
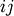 th entry is the cophenetic distance between
original observations
th entry is the cophenetic distance between
original observations 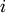 and
and 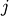 .
.
- scipy.cluster.hierarchy.correspond(Z, Y)¶
Checks if a linkage matrix Z and condensed distance matrix Y could possibly correspond to one another.
They must have the same number of original observations for the check to succeed.
This function is useful as a sanity check in algorithms that make extensive use of linkage and distance matrices that must correspond to the same set of original observations.
Arguments : - Z : ndarray
The linkage matrix to check for correspondance.
- Y : ndarray
The condensed distance matrix to check for correspondance.
Returns : - b : bool
A boolean indicating whether the linkage matrix and distance matrix could possibly correspond to one another.
- scipy.cluster.hierarchy.dendrogram(Z, p=30, truncate_mode=None, color_threshold=None, get_leaves=True, orientation='top', labels=None, count_sort=False, distance_sort=False, show_leaf_counts=True, no_plot=False, no_labels=False, color_list=None, leaf_font_size=None, leaf_rotation=None, leaf_label_func=None, no_leaves=False, show_contracted=False, link_color_func=None)¶
Plots the hiearchical clustering defined by the linkage Z as a dendrogram. The dendrogram illustrates how each cluster is composed by drawing a U-shaped link between a non-singleton cluster and its children. The height of the top of the U-link is the distance between its children clusters. It is also the cophenetic distance between original observations in the two children clusters. It is expected that the distances in Z[:,2] be monotonic, otherwise crossings appear in the dendrogram.
Arguments: Z : ndarray The linkage matrix encoding the hierarchical clustering to render as a dendrogram. See the linkage function for more information on the format of Z.
truncate_mode : string The dendrogram can be hard to read when the original observation matrix from which the linkage is derived is large. Truncation is used to condense the dendrogram. There are several modes:
- None/’none’: no truncation is performed (Default)
- ‘lastp’: the last p non-singleton formed in the linkage
are the only non-leaf nodes in the linkage; they correspond to to rows Z[n-p-2:end] in Z. All other non-singleton clusters are contracted into leaf nodes.
- ‘mlab’: This corresponds to MATLAB(TM) behavior. (not
implemented yet)
- ‘level’/’mtica’: no more than p levels of the
dendrogram tree are displayed. This corresponds to Mathematica(TM) behavior.
- p : int The p parameter for truncate_mode.
- `
color_threshold : double For brevity, let
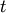 be the color_threshold.
Colors all the descendent links below a cluster node
be the color_threshold.
Colors all the descendent links below a cluster node
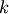 the same color if
the same color if 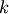 is the first node below
the cut threshold
is the first node below
the cut threshold 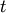 . All links connecting nodes with
distances greater than or equal to the threshold are colored
blue. If
. All links connecting nodes with
distances greater than or equal to the threshold are colored
blue. If 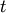 is less than or equal to zero, all nodes
are colored blue. If color_threshold is None or
‘default’, corresponding with MATLAB(TM) behavior, the
threshold is set to 0.7*max(Z[:,2]).
is less than or equal to zero, all nodes
are colored blue. If color_threshold is None or
‘default’, corresponding with MATLAB(TM) behavior, the
threshold is set to 0.7*max(Z[:,2]).get_leaves : bool Includes a list R['leaves']=H in the result dictionary. For each
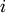 , H[i] == j, cluster node
, H[i] == j, cluster node
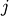 appears in the
appears in the 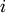 th position in the
left-to-right traversal of the leaves, where
th position in the
left-to-right traversal of the leaves, where 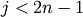 and
and 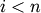 .
.orientation : string The direction to plot the dendrogram, which can be any of the following strings
- ‘top’: plots the root at the top, and plot descendent
links going downwards. (default).
- ‘bottom’: plots the root at the bottom, and plot descendent
links going upwards.
- ‘left’: plots the root at the left, and plot descendent
links going right.
- ‘right’: plots the root at the right, and plot descendent
links going left.
labels : ndarray By default labels is None so the index of the original observation is used to label the leaf nodes.
Otherwise, this is an
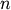 -sized list (or tuple). The
labels[i] value is the text to put under the
-sized list (or tuple). The
labels[i] value is the text to put under the 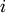 th
leaf node only if it corresponds to an original observation
and not a non-singleton cluster.
th
leaf node only if it corresponds to an original observation
and not a non-singleton cluster.count_sort : string/bool For each node n, the order (visually, from left-to-right) n’s two descendent links are plotted is determined by this parameter, which can be any of the following values:
- False: nothing is done.
- ‘ascending’/True: the child with the minimum number of
original objects in its cluster is plotted first.
- ‘descendent’: the child with the maximum number of
original objects in its cluster is plotted first.
Note distance_sort and count_sort cannot both be True.
distance_sort : string/bool For each node n, the order (visually, from left-to-right) n’s two descendent links are plotted is determined by this parameter, which can be any of the following values:
- False: nothing is done.
- ‘ascending’/True: the child with the minimum distance
between its direct descendents is plotted first.
- ‘descending’: the child with the maximum distance
between its direct descendents is plotted first.
Note distance_sort and count_sort cannot both be True.
show_leaf_counts : bool
When True, leaf nodes representing
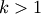 original
observation are labeled with the number of observations they
contain in parentheses.
original
observation are labeled with the number of observations they
contain in parentheses.no_plot : bool When True, the final rendering is not performed. This is useful if only the data structures computed for the rendering are needed or if matplotlib is not available.
no_labels : bool When True, no labels appear next to the leaf nodes in the rendering of the dendrogram.
leaf_label_rotation : double
Specifies the angle (in degrees) to rotate the leaf labels. When unspecified, the rotation based on the number of nodes in the dendrogram. (Default=0)
leaf_font_size : int Specifies the font size (in points) of the leaf labels. When unspecified, the size based on the number of nodes in the dendrogram.
leaf_label_func : lambda or function
When leaf_label_func is a callable function, for each leaf with cluster index
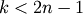 . The function
is expected to return a string with the label for the
leaf.
. The function
is expected to return a string with the label for the
leaf.Indices
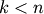 correspond to original observations
while indices
correspond to original observations
while indices 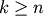 correspond to non-singleton
clusters.
correspond to non-singleton
clusters.For example, to label singletons with their node id and non-singletons with their id, count, and inconsistency coefficient, simply do:
# First define the leaf label function. def llf(id): if id < n: return str(id) else: return '[%d %d %1.2f]' % (id, count, R[n-id,3]) # The text for the leaf nodes is going to be big so force # a rotation of 90 degrees. dendrogram(Z, leaf_label_func=llf, leaf_rotation=90)
show_contracted : bool When True the heights of non-singleton nodes contracted into a leaf node are plotted as crosses along the link connecting that leaf node. This really is only useful when truncation is used (see truncate_mode parameter).
link_color_func : lambda/function When a callable function, link_color_function is called with each non-singleton id corresponding to each U-shaped link it will paint. The function is expected to return the color to paint the link, encoded as a matplotlib color string code.
For example:
dendrogram(Z, link_color_func=lambda k: colors[k])
colors the direct links below each untruncated non-singleton node k using colors[k].
Returns: R : dict A dictionary of data structures computed to render the dendrogram. Its has the following keys:
- ‘icoords’: a list of lists [I1, I2, ..., Ip] where
Ik is a list of 4 independent variable coordinates corresponding to the line that represents the k’th link painted.
- ‘dcoords’: a list of lists [I2, I2, ..., Ip] where
Ik is a list of 4 independent variable coordinates corresponding to the line that represents the k’th link painted.
- ‘ivl’: a list of labels corresponding to the leaf nodes.
- ‘leaves’: for each i, H[i] == j, cluster node
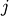 appears in the
appears in the 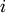 th position in the
left-to-right traversal of the leaves, where
th position in the
left-to-right traversal of the leaves, where 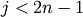 and
and 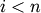 . If
. If 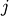 is less than
is less than 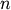 , the
, the
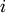 th leaf node corresponds to an original
observation. Otherwise, it corresponds to a non-singleton
cluster.
th leaf node corresponds to an original
observation. Otherwise, it corresponds to a non-singleton
cluster.
- scipy.cluster.hierarchy.fcluster(Z, t, criterion='inconsistent', depth=2, R=None, monocrit=None)¶
Forms flat clusters from the hierarchical clustering defined by the linkage matrix Z. The threshold t is a required parameter.
Arguments : Z : ndarray The hierarchical clustering encoded with the matrix returned by the linkage function.
t : double The threshold to apply when forming flat clusters.
criterion : string (optional) The criterion to use in forming flat clusters. This can be any of the following values:
- ‘inconsistent’: If a cluster node and all its
decendents have an inconsistent value less than or equal to t then all its leaf descendents belong to the same flat cluster. When no non-singleton cluster meets this criterion, every node is assigned to its own cluster. (Default)
- ‘distance’: Forms flat clusters so that the original
observations in each flat cluster have no greater a cophenetic distance than t.
- ‘maxclust’: Finds a minimum threshold r so that
the cophenetic distance between any two original observations in the same flat cluster is no more than r and no more than t flat clusters are formed.
- ‘monocrit’: Forms a flat cluster from a cluster node c
with index i when monocrit[j] <= t.
For example, to threshold on the maximum mean distance as computed in the inconsistency matrix R with a threshold of 0.8 do:
MR = maxRstat(Z, R, 3) cluster(Z, t=0.8, criterion='monocrit', monocrit=MR)
- ‘maxclust_monocrit’: Forms a flat cluster from a
non-singleton cluster node c when monocrit[i] <= r for all cluster indices i below and including c. r is minimized such that no more than t flat clusters are formed. monocrit must be monotonic. For example, to minimize the threshold t on maximum inconsistency values so that no more than 3 flat clusters are formed, do:
MI = maxinconsts(Z, R) cluster(Z, t=3, criterion=’maxclust_monocrit’, monocrit=MI)
- depth : int (optional) The maximum depth to perform the inconsistency calculation. It has no meaning for the other criteria. (default=2)
- R : ndarray (optional) The inconsistency matrix to use for the ‘inconsistent’ criterion. This matrix is computed if not provided.
- monocrit : ndarray (optional) A (n-1) numpy vector of doubles. monocrit[i] is the statistics upon which non-singleton i is thresholded. The monocrit vector must be monotonic, i.e. given a node c with index i, for all node indices j corresponding to nodes below c, monocrit[i] >= monocrit[j].
Returns : - T : ndarray
A vector of length n. T[i] is the flat cluster number to which original observation i belongs.
- scipy.cluster.hierarchy.fclusterdata(X, t, criterion='inconsistent', metric='euclidean', depth=2, method='single', R=None)¶
T = fclusterdata(X, t)
Clusters the original observations in the n by m data matrix X (n observations in m dimensions), using the euclidean distance metric to calculate distances between original observations, performs hierarchical clustering using the single linkage algorithm, and forms flat clusters using the inconsistency method with t as the cut-off threshold.
A one-dimensional numpy array T of length n is returned. T[i] is the index of the flat cluster to which the original observation i belongs.
Arguments : - X : ndarray n by m data matrix with n observations in m dimensions.
- t : double The threshold to apply when forming flat clusters.
- criterion : string Specifies the criterion for forming flat clusters. Valid values are ‘inconsistent’, ‘distance’, or ‘maxclust’ cluster formation algorithms. See fcluster for descriptions.
- method : string The linkage method to use (single, complete, average, weighted, median centroid, ward). See linkage for more information.
- metric : string The distance metric for calculating pairwise distances. See distance.pdist for descriptions and linkage to verify compatibility with the linkage method.
- t : double The cut-off threshold for the cluster function or the maximum number of clusters (criterion=’maxclust’).
- depth : int The maximum depth for the inconsistency calculation. See inconsistent for more information.
- R : ndarray The inconsistency matrix. It will be computed if necessary if it is not passed.
Returns : - T : ndarray A vector of length n. T[i] is the flat cluster number to which original observation i belongs.
Notes
This function is similar to MATLAB(TM) clusterdata function.
- scipy.cluster.hierarchy.from_mlab_linkage(Z)¶
Converts a linkage matrix generated by MATLAB(TM) to a new linkage matrix compatible with this module. The conversion does two things:
- the indices are converted from 1..N to 0..(N-1) form, and
- a fourth column Z[:,3] is added where Z[i,3] is represents the number of original observations (leaves) in the non-singleton cluster i.
This function is useful when loading in linkages from legacy data files generated by MATLAB.
Arguments : - Z : ndarray
A linkage matrix generated by MATLAB(TM)
Returns : - ZS : ndarray
A linkage matrix compatible with this library.
- scipy.cluster.hierarchy.inconsistent(Z, d=2)¶
Calculates inconsistency statistics on a linkage.
Note: This function behaves similarly to the MATLAB(TM) inconsistent function.
Parameters : - d : int
The number of links up to d levels below each non-singleton cluster
- Z : ndarray
The
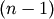 by 4 matrix encoding the linkage
(hierarchical clustering). See linkage documentation
for more information on its form.
by 4 matrix encoding the linkage
(hierarchical clustering). See linkage documentation
for more information on its form.
Returns : - R : ndarray
A
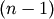 by 5 matrix where the i‘th row
contains the link statistics for the non-singleton cluster
i. The link statistics are computed over the link
heights for links
by 5 matrix where the i‘th row
contains the link statistics for the non-singleton cluster
i. The link statistics are computed over the link
heights for links 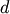 levels below the cluster
i. R[i,0] and R[i,1] are the mean and standard
deviation of the link heights, respectively; R[i,2] is
the number of links included in the calculation; and
R[i,3] is the inconsistency coefficient,
levels below the cluster
i. R[i,0] and R[i,1] are the mean and standard
deviation of the link heights, respectively; R[i,2] is
the number of links included in the calculation; and
R[i,3] is the inconsistency coefficient,![\frac{\mathtt{Z[i,2]}-\mathtt{R[i,0]}}
{R[i,1]}.](_images/math/ff684852e8ebe4bce74756d4ee689701ffe7ffe2.png)
- scipy.cluster.hierarchy.is_isomorphic(T1, T2)¶
Determines if two different cluster assignments T1 and T2 are equivalent.
Arguments : - T1 : ndarray An assignment of singleton cluster ids to flat cluster ids.
- T2 : ndarray An assignment of singleton cluster ids to flat cluster ids.
Returns: - b : boolean Whether the flat cluster assignments T1 and T2 are equivalent.
- scipy.cluster.hierarchy.is_monotonic(Z)¶
Returns True if the linkage passed is monotonic. The linkage is monotonic if for every cluster
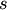 and
and 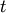 joined, the distance between them is no less than the distance
between any previously joined clusters.
joined, the distance between them is no less than the distance
between any previously joined clusters.Arguments : - Z : ndarray The linkage matrix to check for monotonicity.
Returns : - b : bool A boolean indicating whether the linkage is monotonic.
- scipy.cluster.hierarchy.is_valid_im(R, warning=False, throw=False, name=None)¶
Returns True if the inconsistency matrix passed is valid. It must be a
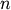 by 4 numpy array of doubles. The standard
deviations R[:,1] must be nonnegative. The link counts
R[:,2] must be positive and no greater than
by 4 numpy array of doubles. The standard
deviations R[:,1] must be nonnegative. The link counts
R[:,2] must be positive and no greater than 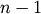 .
.Arguments : - R : ndarray The inconsistency matrix to check for validity.
- warning : bool When True, issues a Python warning if the linkage matrix passed is invalid.
- throw : bool When True, throws a Python exception if the linkage matrix passed is invalid.
- name : string This string refers to the variable name of the invalid linkage matrix.
Returns : - b : bool True iff the inconsistency matrix is valid.
- scipy.cluster.hierarchy.is_valid_linkage(Z, warning=False, throw=False, name=None)¶
Checks the validity of a linkage matrix. A linkage matrix is valid if it is a two dimensional nd-array (type double) with
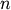 rows and 4 columns. The first two columns must contain indices
between 0 and
rows and 4 columns. The first two columns must contain indices
between 0 and 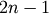 . For a given row i,
. For a given row i,
![0 \leq \mathtt{Z[i,0]} \leq i+n-1](_images/math/54e295d8368b9b6989d49c6e38900f79fafa1117.png) and
and ![0 \leq Z[i,1] \leq i+n-1](_images/math/4a6e6718a2f406018df8646db23512eb1edd97fa.png) (i.e. a cluster cannot join another cluster unless the cluster
being joined has been generated.)
(i.e. a cluster cannot join another cluster unless the cluster
being joined has been generated.)Arguments : - warning : bool When True, issues a Python warning if the linkage matrix passed is invalid.
- throw : bool When True, throws a Python exception if the linkage matrix passed is invalid.
- name : string This string refers to the variable name of the invalid linkage matrix.
Returns : - b : bool
True iff the inconsistency matrix is valid.
- scipy.cluster.hierarchy.leaders(Z, T)¶
(L, M) = leaders(Z, T):
Returns the root nodes in a hierarchical clustering corresponding to a cut defined by a flat cluster assignment vector T. See the fcluster function for more information on the format of T.
For each flat cluster
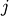 of the
of the 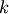 flat clusters
represented in the n-sized flat cluster assignment vector T,
this function finds the lowest cluster node
flat clusters
represented in the n-sized flat cluster assignment vector T,
this function finds the lowest cluster node 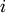 in the linkage
tree Z such that:
in the linkage
tree Z such that:- leaf descendents belong only to flat cluster j
(i.e. T[p]==j for all
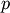 in
in 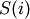 where
where
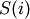 is the set of leaf ids of leaf nodes descendent
with cluster node
is the set of leaf ids of leaf nodes descendent
with cluster node 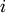 )
) - there does not exist a leaf that is not descendent with
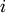 that also belongs to cluster
that also belongs to cluster 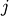 (i.e. T[q]!=j for all
(i.e. T[q]!=j for all 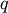 not in
not in 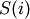 ). If
this condition is violated, T is not a valid cluster
assignment vector, and an exception will be thrown.
). If
this condition is violated, T is not a valid cluster
assignment vector, and an exception will be thrown.
Arguments : - Z : ndarray
The hierarchical clustering encoded as a matrix. See linkage for more information.
- T : ndarray
The flat cluster assignment vector.
Returns : (L, M)
- L : ndarray
The leader linkage node id’s stored as a k-element 1D array where
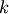 is the number of flat clusters found
in T.
is the number of flat clusters found
in T.L[j]=i is the linkage cluster node id that is the leader of flat cluster with id M[j]. If i < n, i corresponds to an original observation, otherwise it corresponds to a non-singleton cluster.
For example: if L[3]=2 and M[3]=8, the flat cluster with id 8’s leader is linkage node 2.
- M : ndarray
The leader linkage node id’s stored as a k-element 1D array where
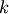 is the number of flat clusters found
in T. This allows the set of flat cluster ids to be
any arbitrary set of
is the number of flat clusters found
in T. This allows the set of flat cluster ids to be
any arbitrary set of 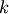 integers.
integers.
- leaf descendents belong only to flat cluster j
(i.e. T[p]==j for all
- scipy.cluster.hierarchy.leaves_list(Z)¶
Returns a list of leaf node ids (corresponding to observation vector index) as they appear in the tree from left to right. Z is a linkage matrix.
Arguments : - Z : ndarray
The hierarchical clustering encoded as a matrix. See linkage for more information.
Returns : - L : ndarray
The list of leaf node ids.
- scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean')¶
- Performs hierarchical/agglomerative clustering on the
condensed distance matrix y. y must be a
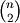 sized
vector where n is the number of original observations paired
in the distance matrix. The behavior of this function is very
similar to the MATLAB(TM) linkage function.
sized
vector where n is the number of original observations paired
in the distance matrix. The behavior of this function is very
similar to the MATLAB(TM) linkage function.A 4 by
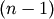 matrix Z is returned. At the
matrix Z is returned. At the
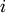 -th iteration, clusters with indices Z[i, 0] and
Z[i, 1] are combined to form cluster
-th iteration, clusters with indices Z[i, 0] and
Z[i, 1] are combined to form cluster 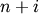 . A
cluster with an index less than
. A
cluster with an index less than 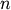 corresponds to one of
the
corresponds to one of
the 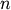 original observations. The distance between
clusters Z[i, 0] and Z[i, 1] is given by Z[i, 2]. The
fourth value Z[i, 3] represents the number of original
observations in the newly formed cluster.
original observations. The distance between
clusters Z[i, 0] and Z[i, 1] is given by Z[i, 2]. The
fourth value Z[i, 3] represents the number of original
observations in the newly formed cluster.The following linkage methods are used to compute the distance
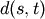 between two clusters
between two clusters 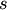 and
and
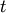 . The algorithm begins with a forest of clusters that
have yet to be used in the hierarchy being formed. When two
clusters
. The algorithm begins with a forest of clusters that
have yet to be used in the hierarchy being formed. When two
clusters 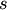 and
and 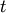 from this forest are combined
into a single cluster
from this forest are combined
into a single cluster 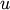 ,
, 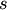 and
and 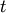 are
removed from the forest, and
are
removed from the forest, and 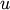 is added to the
forest. When only one cluster remains in the forest, the algorithm
stops, and this cluster becomes the root.
is added to the
forest. When only one cluster remains in the forest, the algorithm
stops, and this cluster becomes the root.A distance matrix is maintained at each iteration. The d[i,j] entry corresponds to the distance between cluster
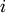 and
and
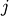 in the original forest.
in the original forest.At each iteration, the algorithm must update the distance matrix to reflect the distance of the newly formed cluster u with the remaining clusters in the forest.
Suppose there are
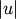 original observations
original observations
![u[0], \ldots, u[|u|-1]](_images/math/fc6a7200130404042ef9469d1371adc30f4d4ffe.png) in cluster
in cluster 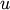 and
and
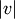 original objects
original objects ![v[0], \ldots, v[|v|-1]](_images/math/d8148db3f0afe74312df26763af4382e5a52b1b8.png) in
cluster
in
cluster 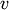 . Recall
. Recall 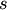 and
and 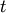 are
combined to form cluster
are
combined to form cluster 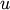 . Let
. Let 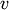 be any
remaining cluster in the forest that is not
be any
remaining cluster in the forest that is not 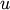 .
.The following are methods for calculating the distance between the newly formed cluster
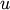 and each
and each 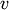 .
.method=’single’ assigns
![d(u,v) = \min(dist(u[i],v[j]))](_images/math/5d7690bb05d67ea02e5015d79e500b80c40733a3.png)
for all points
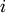 in cluster
in cluster 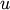 and
and
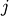 in cluster
in cluster 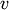 . This is also known as the
Nearest Point Algorithm.
. This is also known as the
Nearest Point Algorithm.method=’complete’ assigns
![d(u, v) = \max(dist(u[i],v[j]))](_images/math/e8281806ed8c8d739e4317b09707c622d9d97635.png)
for all points
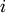 in cluster u and
in cluster u and 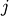 in
cluster
in
cluster 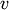 . This is also known by the Farthest Point
Algorithm or Voor Hees Algorithm.
. This is also known by the Farthest Point
Algorithm or Voor Hees Algorithm.method=’average’ assigns
![d(u,v) = \sum_{ij} \frac{d(u[i], v[j])}
{(|u|*|v|)}](_images/math/453fb2bb40a60499bfd7c6c6aaf1086b73395ec1.png)
for all points
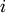 and
and 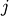 where
where 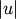 and
and 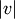 are the cardinalities of clusters
are the cardinalities of clusters 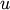 and
and 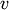 , respectively. This is also called the UPGMA
algorithm. This is called UPGMA.
, respectively. This is also called the UPGMA
algorithm. This is called UPGMA.method=’weighted’ assigns
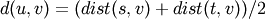
where cluster u was formed with cluster s and t and v is a remaining cluster in the forest. (also called WPGMA)
method=’centroid’ assigns
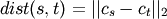
where
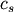 and
and 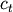 are the centroids of
clusters
are the centroids of
clusters 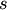 and
and 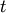 , respectively. When two
clusters
, respectively. When two
clusters 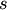 and
and 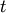 are combined into a new
cluster
are combined into a new
cluster 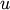 , the new centroid is computed over all the
original objects in clusters
, the new centroid is computed over all the
original objects in clusters 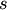 and
and 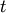 . The
distance then becomes the Euclidean distance between the
centroid of
. The
distance then becomes the Euclidean distance between the
centroid of 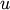 and the centroid of a remaining cluster
and the centroid of a remaining cluster
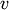 in the forest. This is also known as the UPGMC
algorithm.
in the forest. This is also known as the UPGMC
algorithm.method=’median’ assigns math:d(s,t) like the centroid method. When two clusters
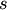 and
and 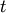 are combined
into a new cluster
are combined
into a new cluster 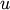 , the average of centroids s and t
give the new centroid
, the average of centroids s and t
give the new centroid 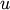 . This is also known as the
WPGMC algorithm.
. This is also known as the
WPGMC algorithm.method=’ward’ uses the Ward variance minimization algorithm. The new entry
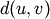 is computed as follows,
is computed as follows,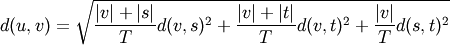
where
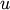 is the newly joined cluster consisting of
clusters
is the newly joined cluster consisting of
clusters 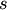 and
and 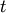 ,
, 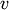 is an unused
cluster in the forest,
is an unused
cluster in the forest, 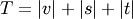 , and
, and
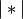 is the cardinality of its argument. This is also
known as the incremental algorithm.
is the cardinality of its argument. This is also
known as the incremental algorithm.
Warning: When the minimum distance pair in the forest is chosen, there may be two or more pairs with the same minimum distance. This implementation may chose a different minimum than the MATLAB(TM) version.
Parameters: - y : ndarray
A condensed or redundant distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of
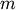 observation vectors in n dimensions may be passed as
an
observation vectors in n dimensions may be passed as
an 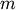 by
by 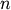 array.
array.
- method : string
The linkage algorithm to use. See the Linkage Methods section below for full descriptions.
- metric : string
The distance metric to use. See the distance.pdist function for a list of valid distance metrics.
Returns : - Z : ndarray
The hierarchical clustering encoded as a linkage matrix.
- scipy.cluster.hierarchy.maxRstat(Z, R, i)¶
Returns the maximum statistic for each non-singleton cluster and its descendents.
Arguments : - Z : ndarray
The hierarchical clustering encoded as a matrix. See linkage for more information.
- R : ndarray
The inconsistency matrix.
- i : int
The column of R to use as the statistic.
Returns : - MR : ndarray Calculates the maximum statistic for the i’th column of the inconsistency matrix R for each non-singleton cluster node. MR[j] is the maximum over R[Q(j)-n, i] where Q(j) the set of all node ids corresponding to nodes below and including j.
- scipy.cluster.hierarchy.maxdists(Z)¶
Returns the maximum distance between any cluster for each non-singleton cluster.
Arguments : - Z : ndarray
The hierarchical clustering encoded as a matrix. See linkage for more information.
Returns : - MD : ndarray A (n-1) sized numpy array of doubles; MD[i] represents the maximum distance between any cluster (including singletons) below and including the node with index i. More specifically, MD[i] = Z[Q(i)-n, 2].max() where Q(i) is the set of all node indices below and including node i.
- scipy.cluster.hierarchy.maxinconsts(Z, R)¶
Returns the maximum inconsistency coefficient for each non-singleton cluster and its descendents.
Arguments : - Z : ndarray
The hierarchical clustering encoded as a matrix. See linkage for more information.
- R : ndarray
The inconsistency matrix.
Returns : - MI : ndarray
A monotonic (n-1)-sized numpy array of doubles.
- scipy.cluster.hierarchy.median(y)¶
Performs median/WPGMC linkage. See linkage for more information on the return structure and algorithm.
The following are common calling conventions:
Z = median(y)
Performs median/WPGMC linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Z = median(X)
Performs median/WPGMC linkage on the observation matrix X using Euclidean distance as the distance metric. See linkage for more information on the return structure and algorithm.
Parameters : - Q : ndarray
A condensed or redundant distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of m observation vectors in n dimensions may be passed as a m by n array.
Returns : - Z : ndarray
The hierarchical clustering encoded as a linkage matrix.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
- scipy.cluster.hierarchy.num_obs_linkage(Z)¶
Returns the number of original observations of the linkage matrix passed.
Arguments : - Z : ndarray
The linkage matrix on which to perform the operation.
Returns : - n : int
The number of original observations in the linkage.
- scipy.cluster.hierarchy.set_link_color_palette(palette)¶
Changes the list of matplotlib color codes to use when coloring links with the dendrogram color_threshold feature.
Arguments : - palette : A list of matplotlib color codes. The order of
the color codes is the order in which the colors are cycled through when color thresholding in the dendrogram.
- scipy.cluster.hierarchy.single(y)¶
Performs single/min/nearest linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Parameters : - y : ndarray
The upper triangular of the distance matrix. The result of pdist is returned in this form.
Returns : - Z : ndarray
The linkage matrix.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
- scipy.cluster.hierarchy.to_mlab_linkage(Z)¶
Converts a linkage matrix Z generated by the linkage function of this module to a MATLAB(TM) compatible one. The return linkage matrix has the last column removed and the cluster indices are converted to 1..N indexing.
Arguments : - Z : ndarray
A linkage matrix generated by this library.
Returns : - ZM : ndarray
A linkage matrix compatible with MATLAB(TM)’s hierarchical clustering functions.
- scipy.cluster.hierarchy.to_tree(Z, rd=False)¶
Converts a hierarchical clustering encoded in the matrix Z (by linkage) into an easy-to-use tree object. The reference r to the root ClusterNode object is returned.
Each ClusterNode object has a left, right, dist, id, and count attribute. The left and right attributes point to ClusterNode objects that were combined to generate the cluster. If both are None then the ClusterNode object is a leaf node, its count must be 1, and its distance is meaningless but set to 0.
Note: This function is provided for the convenience of the library user. ClusterNodes are not used as input to any of the functions in this library.
Parameters : - Z : ndarray The linkage matrix in proper form (see the linkage function documentation).
- r : bool When False, a reference to the root ClusterNode object is returned. Otherwise, a tuple (r,d) is returned. r is a reference to the root node while d is a dictionary mapping cluster ids to ClusterNode references. If a cluster id is less than n, then it corresponds to a singleton cluster (leaf node). See linkage for more information on the assignment of cluster ids to clusters.
Returns : - L : list The pre-order traversal.
- scipy.cluster.hierarchy.ward(y)¶
Performs Ward’s linkage on a condensed or redundant distance matrix. See linkage for more information on the return structure and algorithm.
The following are common calling conventions:
- Z = ward(y) Performs Ward’s linkage on the condensed distance matrix Z. See linkage for more information on the return structure and algorithm.
- Z = ward(X) Performs Ward’s linkage on the observation matrix X using Euclidean distance as the distance metric. See linkage for more information on the return structure and algorithm.
Parameters : - Q : ndarray
A condensed or redundant distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of m observation vectors in n dimensions may be passed as a m by n array.
Returns : - Z : ndarray
The hierarchical clustering encoded as a linkage matrix.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
- scipy.cluster.hierarchy.weighted(y)¶
Performs weighted/WPGMA linkage on the condensed distance matrix y. See linkage for more information on the return structure and algorithm.
Parameters : - y : ndarray
The upper triangular of the distance matrix. The result of pdist is returned in this form.
Returns : - Z : ndarray
A linkage matrix containing the hierarchical clustering. See the linkage function documentation for more information on its structure.
Seealso : - linkage: for advanced creation of hierarchical clusterings.
