Distance computations (scipy.spatial.distance)¶
Function Reference¶
Distance matrix computation from a collection of raw observation vectors stored in a rectangular array.
| Function | Description |
| pdist | pairwise distances between observation vectors. |
| cdist | distances between between two collections of observation vectors. |
| squareform | converts a square distance matrix to a condensed one and vice versa. |
Predicates for checking the validity of distance matrices, both condensed and redundant. Also contained in this module are functions for computing the number of observations in a distance matrix.
| Function | Description |
| is_valid_dm | checks for a valid distance matrix. |
| is_valid_y | checks for a valid condensed distance matrix. |
| num_obs_dm | # of observations in a distance matrix. |
| num_obs_y | # of observations in a condensed distance matrix. |
Distance functions between two vectors u and v. Computing distances over a large collection of vectors is inefficient for these functions. Use pdist for this purpose.
| Function | Description |
| braycurtis | the Bray-Curtis distance. |
| canberra | the Canberra distance. |
| chebyshev | the Chebyshev distance. |
| cityblock | the Manhattan distance. |
| correlation | the Correlation distance. |
| cosine | the Cosine distance. |
| dice | the Dice dissimilarity (boolean). |
| euclidean | the Euclidean distance. |
| hamming | the Hamming distance (boolean). |
| jaccard | the Jaccard distance (boolean). |
| kulsinski | the Kulsinski distance (boolean). |
| mahalanobis | the Mahalanobis distance. |
| matching | the matching dissimilarity (boolean). |
| minkowski | the Minkowski distance. |
| rogerstanimoto | the Rogers-Tanimoto dissimilarity (boolean). |
| russellrao | the Russell-Rao dissimilarity (boolean). |
| seuclidean | the normalized Euclidean distance. |
| sokalmichener | the Sokal-Michener dissimilarity (boolean). |
| sokalsneath | the Sokal-Sneath dissimilarity (boolean). |
| sqeuclidean | the squared Euclidean distance. |
| yule | the Yule dissimilarity (boolean). |
References¶
| [Sta07] | “Statistics toolbox.” API Reference Documentation. The MathWorks. http://www.mathworks.com/access/helpdesk/help/toolbox/stats/. Accessed October 1, 2007. |
| [Mti07] | “Hierarchical clustering.” API Reference Documentation. The Wolfram Research, Inc. http://reference.wolfram.com/mathematica/HierarchicalClustering/tutorial/HierarchicalClustering.html. Accessed October 1, 2007. |
| [Gow69] | Gower, JC and Ross, GJS. “Minimum Spanning Trees and Single Linkage Cluster Analysis.” Applied Statistics. 18(1): pp. 54–64. 1969. |
| [War63] | Ward Jr, JH. “Hierarchical grouping to optimize an objective function.” Journal of the American Statistical Association. 58(301): pp. 236–44. 1963. |
| [Joh66] | Johnson, SC. “Hierarchical clustering schemes.” Psychometrika. 32(2): pp. 241–54. 1966. |
| [Sne62] | Sneath, PH and Sokal, RR. “Numerical taxonomy.” Nature. 193: pp. 855–60. 1962. |
| [Bat95] | Batagelj, V. “Comparing resemblance measures.” Journal of Classification. 12: pp. 73–90. 1995. |
| [Sok58] | Sokal, RR and Michener, CD. “A statistical method for evaluating systematic relationships.” Scientific Bulletins. 38(22): pp. 1409–38. 1958. |
| [Ede79] | Edelbrock, C. “Mixture model tests of hierarchical clustering algorithms: the problem of classifying everybody.” Multivariate Behavioral Research. 14: pp. 367–84. 1979. |
| [Jai88] | Jain, A., and Dubes, R., “Algorithms for Clustering Data.” Prentice-Hall. Englewood Cliffs, NJ. 1988. |
| [Fis36] | Fisher, RA “The use of multiple measurements in taxonomic problems.” Annals of Eugenics, 7(2): 179-188. 1936 |
Copyright Notice¶
Copyright (C) Damian Eads, 2007-2008. New BSD License.
- scipy.spatial.distance.braycurtis(u, v)¶
Computes the Bray-Curtis distance between two n-vectors u and v, which is defined as
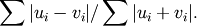
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Bray-Curtis distance between vectors u and v.
- scipy.spatial.distance.canberra(u, v)¶
Computes the Canberra distance between two n-vectors u and v, which is defined as
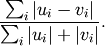
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Canberra distance between vectors u and v.
- scipy.spatial.distance.cdist(XA, XB, metric='euclidean', p=2, V=None, VI=None, w=None)¶
Computes distance between each pair of observation vectors in the Cartesian product of two collections of vectors. XA is a
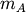 by
by  array while XB is a
array while XB is a 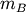 by
by
 array. A
array. A 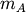 by
by 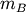 array is
returned. An exception is thrown if XA and XB do not have
the same number of columns.
array is
returned. An exception is thrown if XA and XB do not have
the same number of columns.A rectangular distance matrix Y is returned. For each
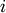 and
and 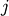 , the metric dist(u=XA[i], v=XB[j]) is computed
and stored in the
, the metric dist(u=XA[i], v=XB[j]) is computed
and stored in the 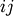 th entry.
th entry.The following are common calling conventions:
Y = cdist(XA, XB, 'euclidean')
Computes the distance between
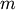 points using
Euclidean distance (2-norm) as the distance metric between the
points. The points are arranged as
points using
Euclidean distance (2-norm) as the distance metric between the
points. The points are arranged as 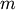
 -dimensional row vectors in the matrix X.
-dimensional row vectors in the matrix X.Y = cdist(XA, XB, 'minkowski', p)
Computes the distances using the Minkowski distance
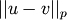 (
(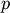 -norm) where
-norm) where 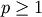 .
.Y = cdist(XA, XB, 'cityblock')
Computes the city block or Manhattan distance between the points.
Y = cdist(XA, XB, 'seuclidean', V=None)
Computes the standardized Euclidean distance. The standardized Euclidean distance between two n-vectors u and v is
![\sqrt{\sum {(u_i-v_i)^2 / V[x_i]}}.](_images/math/5f14770a5e15ad820d65787eb0fedc44f477e58e.png)
- V is the variance vector; V[i] is the variance computed over all
the i’th components of the points. If not passed, it is automatically computed.
Y = cdist(XA, XB, 'sqeuclidean')
Computes the squared Euclidean distance
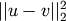 between
the vectors.
between
the vectors.Y = cdist(XA, XB, 'cosine')
Computes the cosine distance between vectors u and v,
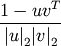
where
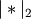 is the 2-norm of its argument *.
is the 2-norm of its argument *.Y = cdist(XA, XB, 'correlation')
Computes the correlation distance between vectors u and v. This is
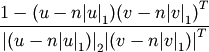
where
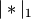 is the Manhattan (or 1-norm) of its
argument, and
is the Manhattan (or 1-norm) of its
argument, and  is the common dimensionality of the
vectors.
is the common dimensionality of the
vectors.Y = cdist(XA, XB, 'hamming')
Computes the normalized Hamming distance, or the proportion of those vector elements between two n-vectors u and v which disagree. To save memory, the matrix X can be of type boolean.
Y = cdist(XA, XB, 'jaccard')
Computes the Jaccard distance between the points. Given two vectors, u and v, the Jaccard distance is the proportion of those elements u[i] and v[i] that disagree where at least one of them is non-zero.
Y = cdist(XA, XB, 'chebyshev')
Computes the Chebyshev distance between the points. The Chebyshev distance between two n-vectors u and v is the maximum norm-1 distance between their respective elements. More precisely, the distance is given by
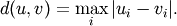
- Y = cdist(XA, XB, 'canberra')
Computes the Canberra distance between the points. The Canberra distance between two points u and v is
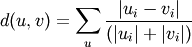
- Y = cdist(XA, XB, 'braycurtis')
Computes the Bray-Curtis distance between the points. The Bray-Curtis distance between two points u and v is
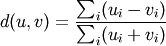
- Y = cdist(XA, XB, 'mahalanobis', VI=None)
Computes the Mahalanobis distance between the points. The Mahalanobis distance between two points u and v is
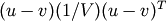 where
where 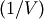 (the VI
variable) is the inverse covariance. If VI is not None,
VI will be used as the inverse covariance matrix.
(the VI
variable) is the inverse covariance. If VI is not None,
VI will be used as the inverse covariance matrix.- Y = cdist(XA, XB, 'yule')
Computes the Yule distance between the boolean vectors. (see yule function documentation)
- Y = cdist(XA, XB, 'matching')
Computes the matching distance between the boolean vectors. (see matching function documentation)
- Y = cdist(XA, XB, 'dice')
Computes the Dice distance between the boolean vectors. (see dice function documentation)
- Y = cdist(XA, XB, 'kulsinski')
Computes the Kulsinski distance between the boolean vectors. (see kulsinski function documentation)
- Y = cdist(XA, XB, 'rogerstanimoto')
Computes the Rogers-Tanimoto distance between the boolean vectors. (see rogerstanimoto function documentation)
- Y = cdist(XA, XB, 'russellrao')
Computes the Russell-Rao distance between the boolean vectors. (see russellrao function documentation)
- Y = cdist(XA, XB, 'sokalmichener')
Computes the Sokal-Michener distance between the boolean vectors. (see sokalmichener function documentation)
- Y = cdist(XA, XB, 'sokalsneath')
Computes the Sokal-Sneath distance between the vectors. (see sokalsneath function documentation)
- Y = cdist(XA, XB, 'wminkowski')
Computes the weighted Minkowski distance between the vectors. (see sokalsneath function documentation)
- Y = cdist(XA, XB, f)
Computes the distance between all pairs of vectors in X using the user supplied 2-arity function f. For example, Euclidean distance between the vectors could be computed as follows:
dm = cdist(XA, XB, (lambda u, v: np.sqrt(((u-v)*(u-v).T).sum())))
Note that you should avoid passing a reference to one of the distance functions defined in this library. For example,:
dm = cdist(XA, XB, sokalsneath)
would calculate the pair-wise distances between the vectors in X using the Python function sokalsneath. This would result in sokalsneath being called
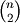 times, which
is inefficient. Instead, the optimized C version is more
efficient, and we call it using the following syntax.:
times, which
is inefficient. Instead, the optimized C version is more
efficient, and we call it using the following syntax.:dm = cdist(XA, XB, 'sokalsneath')
Parameters: - XA : ndarray
An
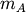 by
by  array of
array of 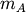 original observations in an
original observations in an  -dimensional space.
-dimensional space.- XB : ndarray
An
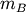 by
by  array of
array of 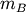 original observations in an
original observations in an  -dimensional space.
-dimensional space.- metric : string or function
The distance metric to use. The distance function can be ‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘wminkowski’, ‘yule’.
- w : ndarray
The weight vector (for weighted Minkowski).
- p : double
The p-norm to apply (for Minkowski, weighted and unweighted)
- V : ndarray
The variance vector (for standardized Euclidean).
- VI : ndarray
The inverse of the covariance matrix (for Mahalanobis).
Returns: - Y : ndarray
A
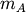 by
by 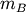 distance matrix.
distance matrix.
- scipy.spatial.distance.chebyshev(u, v)¶
Computes the Chebyshev distance between two n-vectors u and v, which is defined as
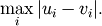
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Chebyshev distance between vectors u and v.
- scipy.spatial.distance.cityblock(u, v)¶
Computes the Manhattan distance between two n-vectors u and v, which is defined as
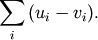
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The City Block distance between vectors u and v.
- scipy.spatial.distance.correlation(u, v)¶
Computes the correlation distance between two n-vectors u and v, which is defined as
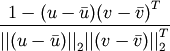
where
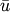 is the mean of a vectors elements and n
is the common dimensionality of u and v.
is the mean of a vectors elements and n
is the common dimensionality of u and v.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The correlation distance between vectors u and v.
- scipy.spatial.distance.cosine(u, v)¶
Computes the Cosine distance between two n-vectors u and v, which is defined as
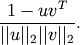
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Cosine distance between vectors u and v.
- scipy.spatial.distance.dice(u, v)¶
Computes the Dice dissimilarity between two boolean n-vectors u and v, which is
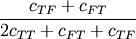
where
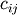 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
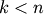 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Dice dissimilarity between vectors u and v.
- scipy.spatial.distance.euclidean(u, v)¶
Computes the Euclidean distance between two n-vectors u and v, which is defined as
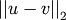
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Euclidean distance between vectors u and v.
- scipy.spatial.distance.hamming(u, v)¶
Computes the Hamming distance between two n-vectors u and v, which is simply the proportion of disagreeing components in u and v. If u and v are boolean vectors, the Hamming distance is
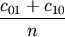
where
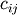 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
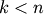 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Hamming distance between vectors u and v.
- scipy.spatial.distance.is_valid_dm(D, tol=0.0, throw=False, name='D', warning=False)¶
Returns True if the variable D passed is a valid distance matrix. Distance matrices must be 2-dimensional numpy arrays containing doubles. They must have a zero-diagonal, and they must be symmetric.
Parameters: - D : ndarray
The candidate object to test for validity.
- tol : double
The distance matrix should be symmetric. tol is the maximum difference between the :math:`ij`th entry and the :math:`ji`th entry for the distance metric to be considered symmetric.
- throw : bool
An exception is thrown if the distance matrix passed is not valid.
- name : string
the name of the variable to checked. This is useful ifa throw is set to True so the offending variable can be identified in the exception message when an exception is thrown.
- warning : boolx
Instead of throwing an exception, a warning message is raised.
Returns: Returns True if the variable D passed is a valid distance matrix. Small numerical differences in D and D.T and non-zeroness of the diagonal are ignored if they are within the tolerance specified by tol.
- scipy.spatial.distance.is_valid_y(y, warning=False, throw=False, name=None)¶
Returns True if the variable y passed is a valid condensed distance matrix. Condensed distance matrices must be 1-dimensional numpy arrays containing doubles. Their length must be a binomial coefficient
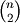 for some positive integer n.
for some positive integer n.Parameters: - y : ndarray
The condensed distance matrix.
- warning : bool
Invokes a warning if the variable passed is not a valid condensed distance matrix. The warning message explains why the distance matrix is not valid. ‘name’ is used when referencing the offending variable.
- throws : throw
Throws an exception if the variable passed is not a valid condensed distance matrix.
- name : bool
Used when referencing the offending variable in the warning or exception message.
- scipy.spatial.distance.jaccard(u, v)¶
Computes the Jaccard-Needham dissimilarity between two boolean n-vectors u and v, which is
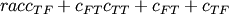
where
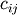 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
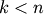 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Jaccard distance between vectors u and v.
- scipy.spatial.distance.kulsinski(u, v)¶
Computes the Kulsinski dissimilarity between two boolean n-vectors u and v, which is defined as
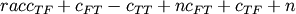
where
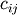 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
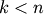 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Kulsinski distance between vectors u and v.
- scipy.spatial.distance.mahalanobis(u, v, VI)¶
Computes the Mahalanobis distance between two n-vectors u and v, which is defiend as
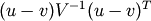
where VI is the inverse covariance matrix
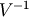 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Mahalanobis distance between vectors u and v.
- scipy.spatial.distance.matching(u, v)¶
Computes the Matching dissimilarity between two boolean n-vectors u and v, which is defined as
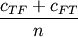
where
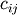 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
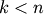 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Matching dissimilarity between vectors u and v.
- scipy.spatial.distance.minkowski(u, v, p)¶
Computes the Minkowski distance between two vectors u and v, defined as
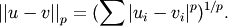
Parameters: - u : ndarray
An n-dimensional vector.
- v : ndarray
An n-dimensional vector.
- p : ndarray
The norm of the difference
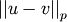 .
.
Returns: - d : double
The Minkowski distance between vectors u and v.
- scipy.spatial.distance.num_obs_dm(d)¶
Returns the number of original observations that correspond to a square, redudant distance matrix D.
Parameters: - d : ndarray
The target distance matrix.
Returns: The number of observations in the redundant distance matrix.
- scipy.spatial.distance.num_obs_y(Y)¶
Returns the number of original observations that correspond to a condensed distance matrix Y.
Parameters: - Y : ndarray
The number of original observations in the condensed observation Y.
Returns: - n : int
The number of observations in the condensed distance matrix passed.
- scipy.spatial.distance.pdist(X, metric='euclidean', p=2, V=None, VI=None)¶
Computes the pairwise distances between m original observations in n-dimensional space. Returns a condensed distance matrix Y. For each
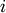 and
and 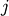 (where
(where 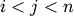 ), the
metric dist(u=X[i], v=X[j]) is computed and stored in the
:math:`ij`th entry.
), the
metric dist(u=X[i], v=X[j]) is computed and stored in the
:math:`ij`th entry.See squareform for information on how to calculate the index of this entry or to convert the condensed distance matrix to a redundant square matrix.
The following are common calling conventions.
Y = pdist(X, 'euclidean')
Computes the distance between m points using Euclidean distance (2-norm) as the distance metric between the points. The points are arranged as m n-dimensional row vectors in the matrix X.
Y = pdist(X, 'minkowski', p)
Computes the distances using the Minkowski distance
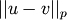 (p-norm) where
(p-norm) where 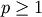 .
.Y = pdist(X, 'cityblock')
Computes the city block or Manhattan distance between the points.
Y = pdist(X, 'seuclidean', V=None)
Computes the standardized Euclidean distance. The standardized Euclidean distance between two n-vectors u and v is
![\sqrt{\sum {(u_i-v_i)^2 / V[x_i]}}.](_images/math/5f14770a5e15ad820d65787eb0fedc44f477e58e.png)
- V is the variance vector; V[i] is the variance computed over all
the i’th components of the points. If not passed, it is automatically computed.
Y = pdist(X, 'sqeuclidean')
Computes the squared Euclidean distance
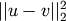 between
the vectors.
between
the vectors.Y = pdist(X, 'cosine')
Computes the cosine distance between vectors u and v,
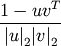
Y = pdist(X, 'correlation')
Computes the correlation distance between vectors u and v. This is
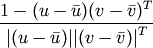
where
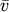 is the mean of the elements of vector v.
is the mean of the elements of vector v.Y = pdist(X, 'hamming')
Computes the normalized Hamming distance, or the proportion of those vector elements between two n-vectors u and v which disagree. To save memory, the matrix X can be of type boolean.
Y = pdist(X, 'jaccard')
Computes the Jaccard distance between the points. Given two vectors, u and v, the Jaccard distance is the proportion of those elements u[i] and v[i] that disagree where at least one of them is non-zero.
Y = pdist(X, 'chebyshev')
Computes the Chebyshev distance between the points. The Chebyshev distance between two n-vectors u and v is the maximum norm-1 distance between their respective elements. More precisely, the distance is given by
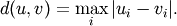
- Y = pdist(X, 'canberra')
Computes the Canberra distance between the points. The Canberra distance between two points u and v is
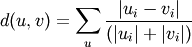
- Y = pdist(X, 'braycurtis')
Computes the Bray-Curtis distance between the points. The Bray-Curtis distance between two points u and v is
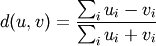
- Y = pdist(X, 'mahalanobis', VI=None)
Computes the Mahalanobis distance between the points. The Mahalanobis distance between two points u and v is
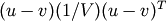 where
where 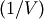 (the VI
variable) is the inverse covariance. If VI is not None,
VI will be used as the inverse covariance matrix.
(the VI
variable) is the inverse covariance. If VI is not None,
VI will be used as the inverse covariance matrix.- Y = pdist(X, 'yule')
Computes the Yule distance between each pair of boolean vectors. (see yule function documentation)
- Y = pdist(X, 'matching')
Computes the matching distance between each pair of boolean vectors. (see matching function documentation)
- Y = pdist(X, 'dice')
Computes the Dice distance between each pair of boolean vectors. (see dice function documentation)
- Y = pdist(X, 'kulsinski')
Computes the Kulsinski distance between each pair of boolean vectors. (see kulsinski function documentation)
- Y = pdist(X, 'rogerstanimoto')
Computes the Rogers-Tanimoto distance between each pair of boolean vectors. (see rogerstanimoto function documentation)
- Y = pdist(X, 'russellrao')
Computes the Russell-Rao distance between each pair of boolean vectors. (see russellrao function documentation)
- Y = pdist(X, 'sokalmichener')
Computes the Sokal-Michener distance between each pair of boolean vectors. (see sokalmichener function documentation)
- Y = pdist(X, 'sokalsneath')
Computes the Sokal-Sneath distance between each pair of boolean vectors. (see sokalsneath function documentation)
- Y = pdist(X, 'wminkowski')
Computes the weighted Minkowski distance between each pair of vectors. (see wminkowski function documentation)
- Y = pdist(X, f)
Computes the distance between all pairs of vectors in X using the user supplied 2-arity function f. For example, Euclidean distance between the vectors could be computed as follows:
dm = pdist(X, (lambda u, v: np.sqrt(((u-v)*(u-v).T).sum())))
Note that you should avoid passing a reference to one of the distance functions defined in this library. For example,:
dm = pdist(X, sokalsneath)
would calculate the pair-wise distances between the vectors in X using the Python function sokalsneath. This would result in sokalsneath being called
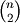 times, which
is inefficient. Instead, the optimized C version is more
efficient, and we call it using the following syntax.:
times, which
is inefficient. Instead, the optimized C version is more
efficient, and we call it using the following syntax.:dm = pdist(X, 'sokalsneath')
Parameters: - X : ndarray
An m by n array of m original observations in an n-dimensional space.
- metric : string or function
The distance metric to use. The distance function can be ‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’.
- w : ndarray
The weight vector (for weighted Minkowski).
- p : double
The p-norm to apply (for Minkowski, weighted and unweighted)
- V : ndarray
The variance vector (for standardized Euclidean).
- VI : ndarray
The inverse of the covariance matrix (for Mahalanobis).
Returns: - Y : ndarray
A condensed distance matrix.
Seealso: - squareform : converts between condensed distance matrices and
square distance matrices.
- scipy.spatial.distance.rogerstanimoto(u, v)¶
Computes the Rogers-Tanimoto dissimilarity between two boolean n-vectors u and v, which is defined as
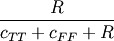
where
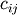 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
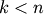 and
and 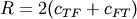 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Rogers-Tanimoto dissimilarity between vectors u and v.
- scipy.spatial.distance.russellrao(u, v)¶
Computes the Russell-Rao dissimilarity between two boolean n-vectors u and v, which is defined as
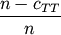
where
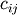 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
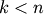 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Russell-Rao dissimilarity between vectors u and v.
- scipy.spatial.distance.seuclidean(u, v, V)¶
Returns the standardized Euclidean distance between two n-vectors u and v. V is an m-dimensional vector of component variances. It is usually computed among a larger collection vectors.
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The standardized Euclidean distance between vectors u and v.
- scipy.spatial.distance.sokalmichener(u, v)¶
Computes the Sokal-Michener dissimilarity between two boolean vectors u and v, which is defined as
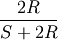
where
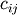 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
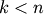 ,
, 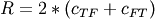 and
and
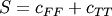 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Sokal-Michener dissimilarity between vectors u and v.
- scipy.spatial.distance.sokalsneath(u, v)¶
Computes the Sokal-Sneath dissimilarity between two boolean vectors u and v,
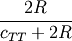
where
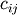 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
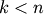 and
and 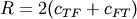 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Sokal-Sneath dissimilarity between vectors u and v.
- scipy.spatial.distance.sqeuclidean(u, v)¶
Computes the squared Euclidean distance between two n-vectors u and v, which is defined as
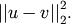
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The squared Euclidean distance between vectors u and v.
- scipy.spatial.distance.squareform(X, force='no', checks=True)¶
Converts a vector-form distance vector to a square-form distance matrix, and vice-versa.
Parameters: - X : ndarray
Either a condensed or redundant distance matrix.
Returns: - Y : ndarray
If a condensed distance matrix is passed, a redundant one is returned, or if a redundant one is passed, a condensed distance matrix is returned.
- force : string
As with MATLAB(TM), if force is equal to ‘tovector’ or ‘tomatrix’, the input will be treated as a distance matrix or distance vector respectively.
- checks : bool
If checks is set to False, no checks will be made for matrix symmetry nor zero diagonals. This is useful if it is known that X - X.T1 is small and diag(X) is close to zero. These values are ignored any way so they do not disrupt the squareform transformation.
- scipy.spatial.distance.wminkowski(u, v, p, w)¶
Computes the weighted Minkowski distance between two vectors u and v, defined as
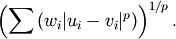
Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.- p : ndarray
The norm of the difference
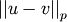 .
.- w : ndarray
The weight vector.
Returns: - d : double
The Minkowski distance between vectors u and v.
- scipy.spatial.distance.yule(u, v)¶
Computes the Yule dissimilarity between two boolean n-vectors u and v, which is defined as
where
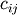 is the number of occurrences of
is the number of occurrences of
![\mathtt{u[k]} = i](_images/math/1f2e6ebb7498423654e0ce52676dc669d0309ce9.png) and
and ![\mathtt{v[k]} = j](_images/math/ca0752041eb1e05ca2b4bb35a62412b5bdad9c32.png) for
for
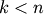 and
and 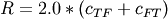 .
.Parameters: - u : ndarray
An
 -dimensional vector.
-dimensional vector.- v : ndarray
An
 -dimensional vector.
-dimensional vector.
Returns: - d : double
The Yule dissimilarity between vectors u and v.
