scipy.signal.slepian¶
-
scipy.signal.slepian(M, width, sym=True)[source]¶ Return a digital Slepian (DPSS) window.
Used to maximize the energy concentration in the main lobe. Also called the digital prolate spheroidal sequence (DPSS).
Parameters: M : int
Number of points in the output window. If zero or less, an empty array is returned.
width : float
Bandwidth
sym : bool, optional
When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.
Returns: w : ndarray
The window, with the maximum value always normalized to 1
References
[R262] D. Slepian & H. O. Pollak: “Prolate spheroidal wave functions, Fourier analysis and uncertainty-I,” Bell Syst. Tech. J., vol.40, pp.43-63, 1961. https://archive.org/details/bstj40-1-43 [R263] H. J. Landau & H. O. Pollak: “Prolate spheroidal wave functions, Fourier analysis and uncertainty-II,” Bell Syst. Tech. J. , vol.40, pp.65-83, 1961. https://archive.org/details/bstj40-1-65 Examples
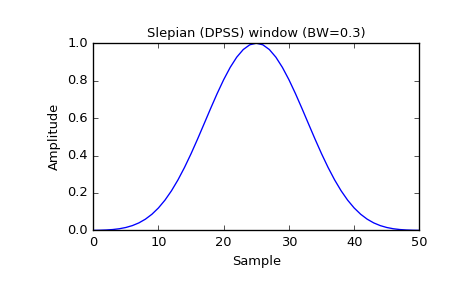
Plot the window and its frequency response:
>>> from scipy import signal >>> from scipy.fftpack import fft, fftshift >>> import matplotlib.pyplot as plt
>>> window = signal.slepian(51, width=0.3) >>> plt.plot(window) >>> plt.title("Slepian (DPSS) window (BW=0.3)") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
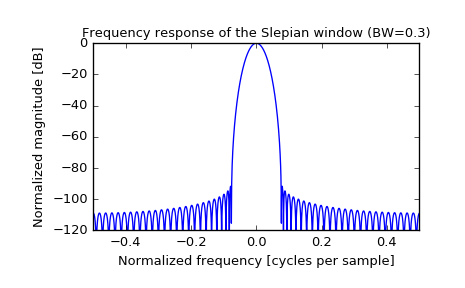
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title("Frequency response of the Slepian window (BW=0.3)") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")