scipy.signal.freqz

scipy.signal.freqz(b, a=1, worN=None, whole=False, plot=None)

Compute the frequency response of a digital filter.

Given the M-order numerator b and N-order denominator a of a digital filter, compute its frequency response:

            jw               -jw               -jwM
   jw    B(e  )  b[0] + b[1]e    + .... + b[M]e
H(e  ) = ---- = -----------------------------------
            jw               -jw               -jwN
         A(e  )  a[0] + a[1]e    + .... + a[N]e

Parameters:

b : array_like

numerator of a linear filter

a : array_like

denominator of a linear filter

worN : {None, int, array_like}, optional

If None (default), then compute at 512 frequencies equally spaced around the unit circle. If a single integer, then compute at that many frequencies. If an array_like, compute the response at the frequencies given (in radians/sample).

whole : bool, optional

Normally, frequencies are computed from 0 to the Nyquist frequency, pi radians/sample (upper-half of unit-circle). If whole is True, compute frequencies from 0 to 2*pi radians/sample.

plot : callable

A callable that takes two arguments. If given, the return parameters w and h are passed to plot. Useful for plotting the frequency response inside freqz.

Returns:

w : ndarray

The normalized frequencies at which h was computed, in radians/sample.

h : ndarray

The frequency response, as complex numbers.

See also

sosfreqz

Notes

Using Matplotlib’s “plot” function as the callable for plot produces unexpected results, this plots the real part of the complex transfer function, not the magnitude. Try lambda w, h: plot(w, abs(h)).

Examples

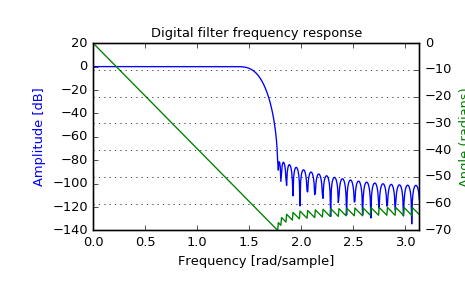
>>> from scipy import signal
>>> b = signal.firwin(80, 0.5, window=('kaiser', 8))
>>> w, h = signal.freqz(b)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> plt.title('Digital filter frequency response')
>>> ax1 = fig.add_subplot(111)

>>> plt.plot(w, 20 * np.log10(abs(h)), 'b')
>>> plt.ylabel('Amplitude [dB]', color='b')
>>> plt.xlabel('Frequency [rad/sample]')

>>> ax2 = ax1.twinx()
>>> angles = np.unwrap(np.angle(h))
>>> plt.plot(w, angles, 'g')
>>> plt.ylabel('Angle (radians)', color='g')
>>> plt.grid()
>>> plt.axis('tight')
>>> plt.show()

(Source code)