scipy.signal.dbode¶
- scipy.signal.dbode(system, w=None, n=100)[source]¶
Calculate Bode magnitude and phase data of a discrete-time system.
Parameters: system : an instance of the LTI class or a tuple describing the system.
The following gives the number of elements in the tuple and the interpretation:
- 1 (instance of dlti)
- 2 (num, den, dt)
- 3 (zeros, poles, gain, dt)
- 4 (A, B, C, D, dt)
w : array_like, optional
Array of frequencies (in radians/sample). Magnitude and phase data is calculated for every value in this array. If not given a reasonable set will be calculated.
n : int, optional
Number of frequency points to compute if w is not given. The n frequencies are logarithmically spaced in an interval chosen to include the influence of the poles and zeros of the system.
Returns: w : 1D ndarray
Frequency array [rad/time_unit]
mag : 1D ndarray
Magnitude array [dB]
phase : 1D ndarray
Phase array [deg]
Notes
If (num, den) is passed in for system, coefficients for both the numerator and denominator should be specified in descending exponent order (e.g. z^2 + 3z + 5 would be represented as [1, 3, 5]).
New in version 0.18.0.
Examples
>>> from scipy import signal >>> import matplotlib.pyplot as plt
Transfer function: H(z) = 1 / (z^2 + 2z + 3)
>>> sys = signal.TransferFunction([1], [1, 2, 3], dt=0.05)
Equivalent: sys.bode()
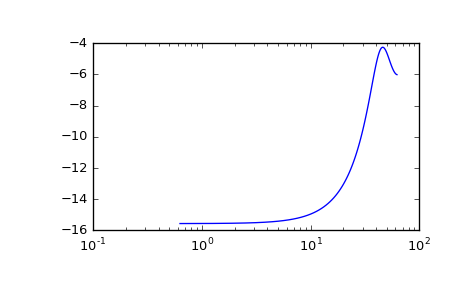
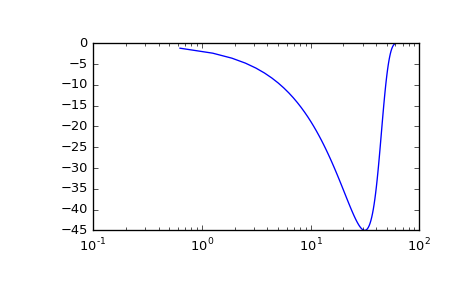
>>> w, mag, phase = signal.dbode(sys)
>>> plt.figure() >>> plt.semilogx(w, mag) # Bode magnitude plot >>> plt.figure() >>> plt.semilogx(w, phase) # Bode phase plot >>> plt.show()