scipy.signal.correlate¶
- scipy.signal.correlate(in1, in2, mode='full')[source]¶
Cross-correlate two N-dimensional arrays.
Cross-correlate in1 and in2, with the output size determined by the mode argument.
Parameters: in1 : array_like
First input.
in2 : array_like
Second input. Should have the same number of dimensions as in1. If operating in ‘valid’ mode, either in1 or in2 must be at least as large as the other in every dimension.
mode : str {‘full’, ‘valid’, ‘same’}, optional
A string indicating the size of the output:
- full
The output is the full discrete linear cross-correlation of the inputs. (Default)
- valid
The output consists only of those elements that do not rely on the zero-padding.
- same
The output is the same size as in1, centered with respect to the ‘full’ output.
Returns: correlate : array
An N-dimensional array containing a subset of the discrete linear cross-correlation of in1 with in2.
Notes
The correlation z of two d-dimensional arrays x and y is defined as:
- z[...,k,...] = sum[..., i_l, ...]
- x[..., i_l,...] * conj(y[..., i_l + k,...])
Examples
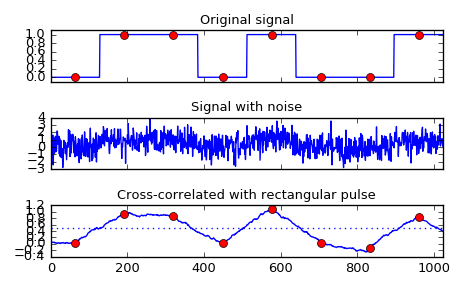
Implement a matched filter using cross-correlation, to recover a signal that has passed through a noisy channel.
>>> from scipy import signal >>> sig = np.repeat([0., 1., 1., 0., 1., 0., 0., 1.], 128) >>> sig_noise = sig + np.random.randn(len(sig)) >>> corr = signal.correlate(sig_noise, np.ones(128), mode='same') / 128
>>> import matplotlib.pyplot as plt >>> clock = np.arange(64, len(sig), 128) >>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, sharex=True) >>> ax_orig.plot(sig) >>> ax_orig.plot(clock, sig[clock], 'ro') >>> ax_orig.set_title('Original signal') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_corr.plot(corr) >>> ax_corr.plot(clock, corr[clock], 'ro') >>> ax_corr.axhline(0.5, ls=':') >>> ax_corr.set_title('Cross-correlated with rectangular pulse') >>> ax_orig.margins(0, 0.1) >>> fig.tight_layout() >>> fig.show()