scipy.signal.coherence

scipy.signal.coherence(x, y, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend='constant', axis=-1)

Estimate the magnitude squared coherence estimate, Cxy, of discrete-time signals X and Y using Welch’s method.

Cxy = abs(Pxy)**2/(Pxx*Pyy), where Pxx and Pyy are power spectral density estimates of X and Y, and Pxy is the cross spectral density estimate of X and Y.

Parameters:

x : array_like

Time series of measurement values

y : array_like

Time series of measurement values

fs : float, optional

Sampling frequency of the x and y time series. Defaults to 1.0.

window : str or tuple or array_like, optional

Desired window to use. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length will be used for nperseg. Defaults to ‘hann’.

nperseg : int, optional

Length of each segment. Defaults to 256.

noverlap: int, optional

Number of points to overlap between segments. If None, noverlap = nperseg // 2. Defaults to None.

nfft : int, optional

Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.

detrend : str or function or False, optional

Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to detrend. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to ‘constant’.

axis : int, optional

Axis along which the coherence is computed for both inputs; the default is over the last axis (i.e. axis=-1).

Returns:

f : ndarray

Array of sample frequencies.

Cxy : ndarray

Magnitude squared coherence of x and y.

See also

periodogram

Simple, optionally modified periodogram

lombscargle

Lomb-Scargle periodogram for unevenly sampled data

welch

Power spectral density by Welch’s method.

csd

Cross spectral density by Welch’s method.

Notes

An appropriate amount of overlap will depend on the choice of window and on your requirements. For the default ‘hann’ window an overlap of 50% is a reasonable trade off between accurately estimating the signal power, while not over counting any of the data. Narrower windows may require a larger overlap.

New in version 0.16.0.

References

[R191]

P. Welch, “The use of the fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms”, IEEE Trans. Audio Electroacoust. vol. 15, pp. 70-73, 1967.

[R192]

Stoica, Petre, and Randolph Moses, “Spectral Analysis of Signals” Prentice Hall, 2005

Examples

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

Generate two test signals with some common features.

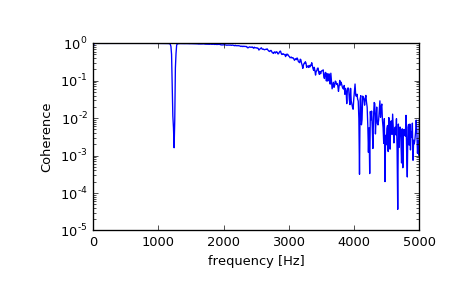
>>> fs = 10e3
>>> N = 1e5
>>> amp = 20
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> b, a = signal.butter(2, 0.25, 'low')
>>> x = np.random.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> y = signal.lfilter(b, a, x)
>>> x += amp*np.sin(2*np.pi*freq*time)
>>> y += np.random.normal(scale=0.1*np.sqrt(noise_power), size=time.shape)

Compute and plot the coherence.

>>> f, Cxy = signal.coherence(x, y, fs, nperseg=1024)
>>> plt.semilogy(f, Cxy)
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Coherence')
>>> plt.show()

(Source code)