scipy.interpolate.CubicSpline¶
- class scipy.interpolate.CubicSpline(x, y, axis=0, bc_type='not-a-knot', extrapolate=None)[source]¶
Cubic spline data interpolator.
Interpolate data with a piecewise cubic polynomial which is twice continuously differentiable [R53]. The result is represented as a PPoly instance with breakpoints matching the given data.
Parameters: x : array_like, shape (n,)
1-d array containing values of the independent variable. Values must be real, finite and in strictly increasing order.
y : array_like
axis : int, optional
Axis along which y is assumed to be varying. Meaning that for x[i] the corresponding values are np.take(y, i, axis=axis). Default is 0.
bc_type : string or 2-tuple, optional
Boundary condition type. Two additional equations, given by the boundary conditions, are required to determine all coefficients of polynomials on each segment [R54].
If bc_type is a string, then the specified condition will be applied at both ends of a spline. Available conditions are:
- ‘not-a-knot’ (default): The first and second segment at a curve end are the same polynomial. It is a good default when there is no information on boundary conditions.
- ‘periodic’: The interpolated functions is assumed to be periodic of period x[-1] - x[0]. The first and last value of y must be identical: y[0] == y[-1]. This boundary condition will result in y'[0] == y'[-1] and y''[0] == y''[-1].
- ‘clamped’: The first derivative at curves ends are zero. Assuming a 1D y, bc_type=((1, 0.0), (1, 0.0)) is the same condition.
- ‘natural’: The second derivative at curve ends are zero. Assuming a 1D y, bc_type=((2, 0.0), (2, 0.0)) is the same condition.
If bc_type is a 2-tuple, the first and the second value will be applied at the curve start and end respectively. The tuple values can be one of the previously mentioned strings (except ‘periodic’) or a tuple (order, deriv_values) allowing to specify arbitrary derivatives at curve ends:
- order: the derivative order, 1 or 2.
- deriv_value: array_like containing derivative values, shape must be the same as y, excluding axis dimension. For example, if y is 1D, then deriv_value must be a scalar. If y is 3D with the shape (n0, n1, n2) and axis=2, then deriv_value must be 2D and have the shape (n0, n1).
extrapolate : {bool, ‘periodic’, None}, optional
If bool, determines whether to extrapolate to out-of-bounds points based on first and last intervals, or to return NaNs. If ‘periodic’, periodic extrapolation is used. If None (default), extrapolate is set to ‘periodic’ for bc_type='periodic' and to True otherwise.
See also
Notes
Parameters bc_type and interpolate work independently, i.e. the former controls only construction of a spline, and the latter only evaluation.
When a boundary condition is ‘not-a-knot’ and n = 2, it is replaced by a condition that the first derivative is equal to the linear interpolant slope. When both boundary conditions are ‘not-a-knot’ and n = 3, the solution is sought as a parabola passing through given points.
When ‘not-a-knot’ boundary conditions is applied to both ends, the resulting spline will be the same as returned by splrep (with s=0) and InterpolatedUnivariateSpline, but these two methods use a representation in B-spline basis.
New in version 0.18.0.
References
[R53] (1, 2) Cubic Spline Interpolation on Wikiversity. [R54] (1, 2) Carl de Boor, “A Practical Guide to Splines”, Springer-Verlag, 1978. Examples
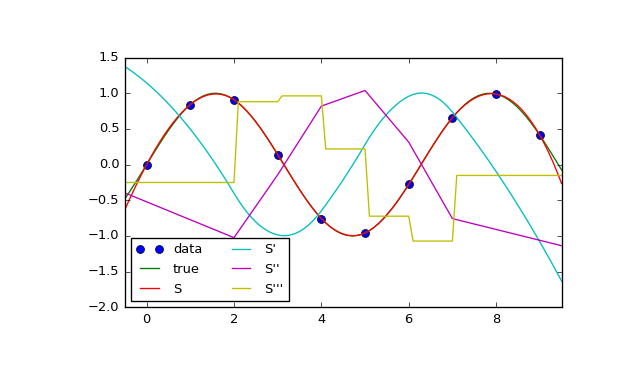
In this example the cubic spline is used to interpolate a sampled sinusoid. You can see that the spline continuity property holds for the first and second derivatives and violates only for the third derivative.
>>> from scipy.interpolate import CubicSpline >>> import matplotlib.pyplot as plt >>> x = np.arange(10) >>> y = np.sin(x) >>> cs = CubicSpline(x, y) >>> xs = np.arange(-0.5, 9.6, 0.1) >>> plt.figure(figsize=(6.5, 4)) >>> plt.plot(x, y, 'o', label='data') >>> plt.plot(xs, np.sin(xs), label='true') >>> plt.plot(xs, cs(xs), label="S") >>> plt.plot(xs, cs(xs, 1), label="S'") >>> plt.plot(xs, cs(xs, 2), label="S''") >>> plt.plot(xs, cs(xs, 3), label="S'''") >>> plt.xlim(-0.5, 9.5) >>> plt.legend(loc='lower left', ncol=2) >>> plt.show()
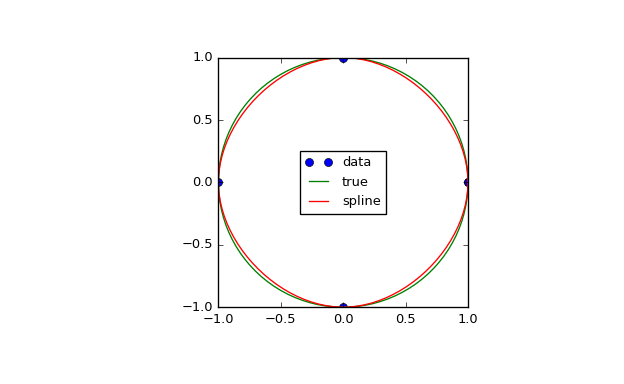
In the second example, the unit circle is interpolated with a spline. A periodic boundary condition is used. You can see that the first derivative values, ds/dx=0, ds/dy=1 at the periodic point (1, 0) are correctly computed. Note that a circle cannot be exactly represented by a cubic spline. To increase precision, more breakpoints would be required.
>>> theta = 2 * np.pi * np.linspace(0, 1, 5) >>> y = np.c_[np.cos(theta), np.sin(theta)] >>> cs = CubicSpline(theta, y, bc_type='periodic') >>> print("ds/dx={:.1f} ds/dy={:.1f}".format(cs(0, 1)[0], cs(0, 1)[1])) ds/dx=0.0 ds/dy=1.0 >>> xs = 2 * np.pi * np.linspace(0, 1, 100) >>> plt.figure(figsize=(6.5, 4)) >>> plt.plot(y[:, 0], y[:, 1], 'o', label='data') >>> plt.plot(np.cos(xs), np.sin(xs), label='true') >>> plt.plot(cs(xs)[:, 0], cs(xs)[:, 1], label='spline') >>> plt.axes().set_aspect('equal') >>> plt.legend(loc='center') >>> plt.show()
The third example is the interpolation of a polynomial y = x**3 on the interval 0 <= x<= 1. A cubic spline can represent this function exactly. To achieve that we need to specify values and first derivatives at endpoints of the interval. Note that y’ = 3 * x**2 and thus y’(0) = 0 and y’(1) = 3.
>>> cs = CubicSpline([0, 1], [0, 1], bc_type=((1, 0), (1, 3))) >>> x = np.linspace(0, 1) >>> np.allclose(x**3, cs(x)) True
Attributes
x (ndarray, shape (n,)) Breakpoints. The same x which was passed to the constructor. c (ndarray, shape (4, n-1, ...)) Coefficients of the polynomials on each segment. The trailing dimensions match the dimensions of y, excluding axis. For example, if y is 1-d, then c[k, i] is a coefficient for (x-x[i])**(3-k) on the segment between x[i] and x[i+1]. axis (int) Interpolation axis. The same axis which was passed to the constructor. Methods
__call__(x[, nu, extrapolate]) Evaluate the piecewise polynomial or its derivative. derivative([nu]) Construct a new piecewise polynomial representing the derivative. antiderivative([nu]) Construct a new piecewise polynomial representing the antiderivative. integrate(a, b[, extrapolate]) Compute a definite integral over a piecewise polynomial. roots([discontinuity, extrapolate]) Find real roots of the the piecewise polynomial.
