scipy.signal.butter

scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba')

Butterworth digital and analog filter design.

Design an Nth order digital or analog Butterworth filter and return the filter coefficients.

Parameters:

N : int

The order of the filter.

Wn : array_like

A scalar or length-2 sequence giving the critical frequencies. For a Butterworth filter, this is the point at which the gain drops to 1/sqrt(2) that of the passband (the “-3 dB point”). For digital filters, Wn is normalized from 0 to 1, where 1 is the Nyquist frequency, pi radians/sample. (Wn is thus in half-cycles / sample.) For analog filters, Wn is an angular frequency (e.g. rad/s).

btype : {‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional

The type of filter. Default is ‘lowpass’.

analog : bool, optional

When True, return an analog filter, otherwise a digital filter is returned.

output : {‘ba’, ‘zpk’, ‘sos’}, optional

Type of output: numerator/denominator (‘ba’), pole-zero (‘zpk’), or second-order sections (‘sos’). Default is ‘ba’.

Returns:

b, a : ndarray, ndarray

Numerator (b) and denominator (a) polynomials of the IIR filter. Only returned if output='ba'.

z, p, k : ndarray, ndarray, float

Zeros, poles, and system gain of the IIR filter transfer function. Only returned if output='zpk'.

sos : ndarray

Second-order sections representation of the IIR filter. Only returned if output=='sos'.

See also

buttord

Notes

The Butterworth filter has maximally flat frequency response in the passband.

The 'sos' output parameter was added in 0.16.0.

Examples

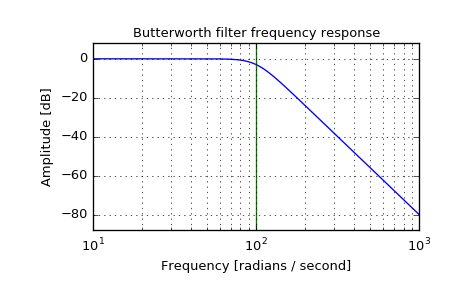
Plot the filter’s frequency response, showing the critical points:

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Butterworth filter frequency response')
>>> plt.xlabel('Frequency [radians / second]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.show()

(Source code)