scipy.signal.blackman¶
- scipy.signal.blackman(M, sym=True)[source]¶
Return a Blackman window.
The Blackman window is a taper formed by using the first three terms of a summation of cosines. It was designed to have close to the minimal leakage possible. It is close to optimal, only slightly worse than a Kaiser window.
Parameters: M : int
Number of points in the output window. If zero or less, an empty array is returned.
sym : bool, optional
When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.
Returns: w : ndarray
The window, with the maximum value normalized to 1 (though the value 1 does not appear if M is even and sym is True).
Notes
The Blackman window is defined as
\[w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)\]Most references to the Blackman window come from the signal processing literature, where it is used as one of many windowing functions for smoothing values. It is also known as an apodization (which means “removing the foot”, i.e. smoothing discontinuities at the beginning and end of the sampled signal) or tapering function. It is known as a “near optimal” tapering function, almost as good (by some measures) as the Kaiser window.
References
[R169] Blackman, R.B. and Tukey, J.W., (1958) The measurement of power spectra, Dover Publications, New York. [R170] Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999, pp. 468-471. Examples
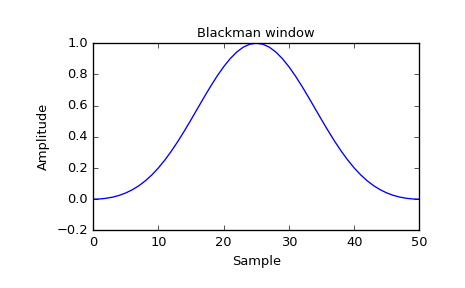
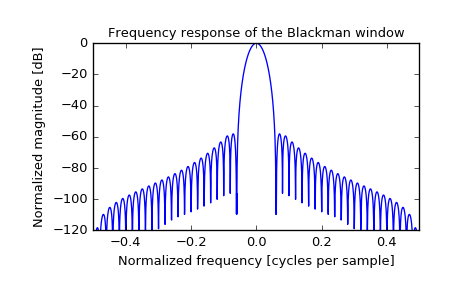
Plot the window and its frequency response:
>>> from scipy import signal >>> from scipy.fftpack import fft, fftshift >>> import matplotlib.pyplot as plt
>>> window = signal.blackman(51) >>> plt.plot(window) >>> plt.title("Blackman window") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title("Frequency response of the Blackman window") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")