scipy.signal.convolve¶
- scipy.signal.convolve(in1, in2, mode='full')[source]¶
Convolve two N-dimensional arrays.
Convolve in1 and in2, with the output size determined by the mode argument.
Parameters: in1 : array_like
First input.
in2 : array_like
Second input. Should have the same number of dimensions as in1; if sizes of in1 and in2 are not equal then in1 has to be the larger array.
mode : str {‘full’, ‘valid’, ‘same’}, optional
A string indicating the size of the output:
- full
The output is the full discrete linear convolution of the inputs. (Default)
- valid
The output consists only of those elements that do not rely on the zero-padding.
- same
The output is the same size as in1, centered with respect to the ‘full’ output.
Returns: convolve : array
An N-dimensional array containing a subset of the discrete linear convolution of in1 with in2.
See also
- numpy.polymul
- performs polynomial multiplication (same operation, but also accepts poly1d objects)
Examples
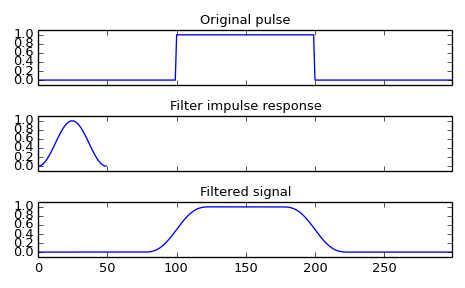
Smooth a square pulse using a Hann window:
>>> from scipy import signal >>> sig = np.repeat([0., 1., 0.], 100) >>> win = signal.hann(50) >>> filtered = signal.convolve(sig, win, mode='same') / sum(win)
>>> import matplotlib.pyplot as plt >>> fig, (ax_orig, ax_win, ax_filt) = plt.subplots(3, 1, sharex=True) >>> ax_orig.plot(sig) >>> ax_orig.set_title('Original pulse') >>> ax_orig.margins(0, 0.1) >>> ax_win.plot(win) >>> ax_win.set_title('Filter impulse response') >>> ax_win.margins(0, 0.1) >>> ax_filt.plot(filtered) >>> ax_filt.set_title('Filtered signal') >>> ax_filt.margins(0, 0.1) >>> fig.tight_layout() >>> fig.show()