Continuous Statistical Distributions¶
Overview¶
All distributions will have location (L) and Scale (S) parameters
along with any shape parameters needed, the names for the shape
parameters will vary. Standard form for the distributions will be
given where 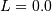 and
and 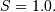 The nonstandard forms can be obtained for the various functions using
(note
The nonstandard forms can be obtained for the various functions using
(note  is a standard uniform random variate).
is a standard uniform random variate).
| Function Name | Standard Function | Transformation |
|---|---|---|
| Cumulative Distribution Function (CDF) | 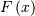 |
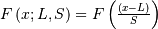 |
| Probability Density Function (PDF) | 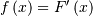 |
 |
| Percent Point Function (PPF) | 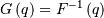 |
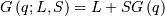 |
| Probability Sparsity Function (PSF) |  |
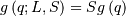 |
| Hazard Function (HF) | 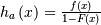 |
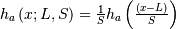 |
| Cumulative Hazard Functon (CHF) | 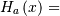 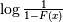 |
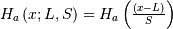 |
| Survival Function (SF) | 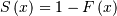 |
 |
| Inverse Survival Function (ISF) | 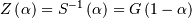 |
 |
| Moment Generating Function (MGF) | ![M_{Y}\left(t\right)=E\left[e^{Yt}\right]](../../_images/math/6e604d279762c38bd58c41bf573dfd37f4797d11.png) |
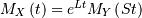 |
| Random Variates | 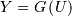 |
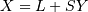 |
| (Differential) Entropy | ![h\left[Y\right]=-\int f\left(y\right)\log f\left(y\right)dy](../../_images/math/a5851cbbaa9271c2bf384144a45ba7eb7df3aa71.png) |
![h\left[X\right]=h\left[Y\right]+\log S](../../_images/math/27c61efaaa283e411c161510a533c80f86fd986a.png) |
| (Non-central) Moments | ![\mu_{n}^{\prime}=E\left[Y^{n}\right]](../../_images/math/0a758ec8a9781a563466d64d60e9b258fcc0fa68.png) |
![E\left[X^{n}\right]=L^{n}\sum_{k=0}^{N}\left(\begin{array}{c} n\\ k\end{array}\right)\left(\frac{S}{L}\right)^{k}\mu_{k}^{\prime}](../../_images/math/3385a8aec8334c4b30f9d7de447228b01c098bab.png) |
| Central Moments | ![\mu_{n}=E\left[\left(Y-\mu\right)^{n}\right]](../../_images/math/88c93d947f4ef318763e1be1e1461d60507b6f2f.png) |
![E\left[\left(X-\mu_{X}\right)^{n}\right]=S^{n}\mu_{n}](../../_images/math/c47712eb3131ce066b7e02b1f465bd090ffbd280.png) |
| mean (mode, median), var | 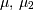 |
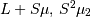 |
| skewness, kurtosis | 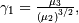 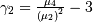 |
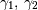 |
Moments¶
Non-central moments are defined using the PDF
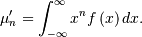
Note, that these can always be computed using the PPF. Substitute 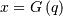 in the above equation and get
in the above equation and get
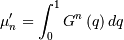
which may be easier to compute numerically. Note that 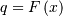 so that
so that 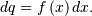 Central moments are computed similarly
Central moments are computed similarly 
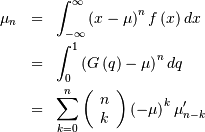
In particular
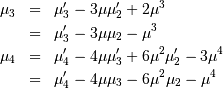
Skewness is defined as

while (Fisher) kurtosis is
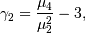
so that a normal distribution has a kurtosis of zero.
Median and mode¶
The median, 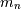 is defined as the point at which half of the density is on one side
and half on the other. In other words,
is defined as the point at which half of the density is on one side
and half on the other. In other words, 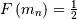 so that
so that
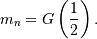
In addition, the mode, 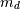 , is defined as the value for which the probability density function
reaches it’s peak
, is defined as the value for which the probability density function
reaches it’s peak
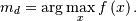
Fitting data¶
To fit data to a distribution, maximizing the likelihood function is common. Alternatively, some distributions have well-known minimum variance unbiased estimators. These will be chosen by default, but the likelihood function will always be available for minimizing.
If  is the PDF of a random-variable where
is the PDF of a random-variable where 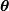 is a vector of parameters ( e.g.
is a vector of parameters ( e.g. 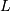 and
and 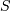 ), then for a collection of
), then for a collection of 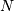 independent samples from this distribution, the joint distribution the
random vector
independent samples from this distribution, the joint distribution the
random vector  is
is
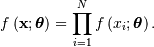
The maximum likelihood estimate of the parameters 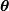 are the parameters which maximize this function with
are the parameters which maximize this function with  fixed and given by the data:
fixed and given by the data:

Where
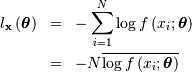
Note that if 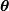 includes only shape parameters, the location and scale-parameters can
be fit by replacing
includes only shape parameters, the location and scale-parameters can
be fit by replacing 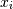 with
with 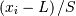 in the log-likelihood function adding
in the log-likelihood function adding 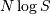 and minimizing, thus
and minimizing, thus
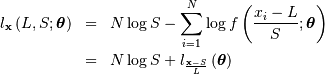
If desired, sample estimates for 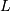 and
and 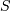 (not necessarily maximum likelihood estimates) can be obtained from
samples estimates of the mean and variance using
(not necessarily maximum likelihood estimates) can be obtained from
samples estimates of the mean and variance using
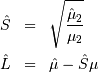
where 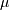 and
and 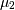 are assumed known as the mean and variance of the untransformed distribution (when
are assumed known as the mean and variance of the untransformed distribution (when 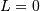 and
and 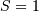 ) and
) and
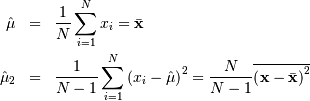
References¶
- Documentation for ranlib, rv2, cdflib
- Eric Weisstein~s world of mathematics http://mathworld.wolfram.com/, http://mathworld.wolfram.com/topics/StatisticalDistributions.html
- Documentation to Regress+ by Michael McLaughlin item Engineering and Statistics Handbook (NIST), http://www.itl.nist.gov/div898/handbook/index.htm
- Documentation for DATAPLOT from NIST, http://www.itl.nist.gov/div898/software/dataplot/distribu.htm
- Norman Johnson, Samuel Kotz, and N. Balakrishnan Continuous Univariate Distributions, second edition, Volumes I and II, Wiley & Sons, 1994.
Alpha¶
One shape parameters 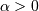 (parameter
(parameter  in DATAPLOT
is a scale-parameter). Standard form is
in DATAPLOT
is a scale-parameter). Standard form is 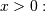
![\begin{eqnarray*} f\left(x;\alpha\right) & = & \frac{1}{x^{2}\Phi\left(\alpha\right)\sqrt{2\pi}}\exp\left(-\frac{1}{2}\left(\alpha-\frac{1}{x}\right)^{2}\right)\\ F\left(x;\alpha\right) & = & \frac{\Phi\left(\alpha-\frac{1}{x}\right)}{\Phi\left(\alpha\right)}\\ G\left(q;\alpha\right) & = & \left[\alpha-\Phi^{-1}\left(q\Phi\left(\alpha\right)\right)\right]^{-1}\end{eqnarray*}](../../_images/math/d87789885aa156d280f7f6d9439f22acf474700f.png)
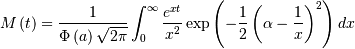
No moments?
![l_{\mathbf{x}}\left(\alpha\right)=N\log\left[\Phi\left(\alpha\right)\sqrt{2\pi}\right]+2N\overline{\log\mathbf{x}}+\frac{N}{2}\alpha^{2}-\alpha\overline{\mathbf{x}^{-1}}+\frac{1}{2}\overline{\mathbf{x}^{-2}}](../../_images/math/2425a91e76f5303c7d10b235d00e8574e0b9d91b.png)
Beta Prime¶
Defined over 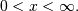
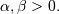 (Note the CDF evaluation uses Eq. 3.194.1 on pg. 313 of Gradshteyn &
Ryzhik (sixth edition).
(Note the CDF evaluation uses Eq. 3.194.1 on pg. 313 of Gradshteyn &
Ryzhik (sixth edition).
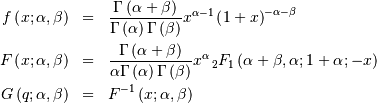
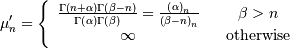
Therefore,
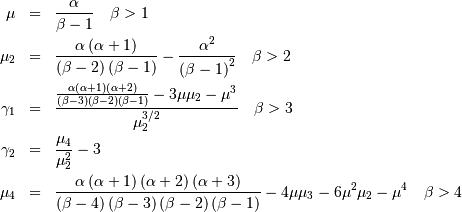
Chi-squared¶
This is the gamma distribution with 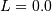 and
and 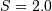 and
and 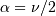 where
where  is called the degrees of freedom. If
is called the degrees of freedom. If 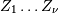 are all standard normal distributions, then
are all standard normal distributions, then 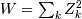 has (standard) chi-square distribution with
has (standard) chi-square distribution with  degrees of freedom.
degrees of freedom.
The standard form (most often used in standard form only) is 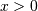
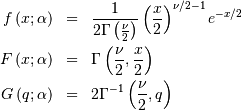
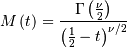
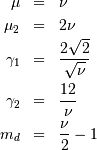
Doubly Non-central F*¶
Doubly Non-central t*¶
Erlang¶
This is just the Gamma distribution with shape parameter  an integer.
an integer.
Exponential¶
This is a special case of the Gamma (and Erlang) distributions with
shape parameter 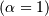 and the same location and scale parameters. The standard form is
therefore (
and the same location and scale parameters. The standard form is
therefore ( 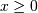 )
)
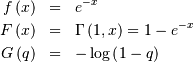
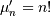
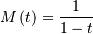
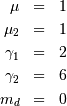
![h\left[X\right]=1.](../../_images/math/5cb0bd3221c1e09f390ada1b0f7ccad9001b96cb.png)
Fatigue Life (Birnbaum-Sanders)¶
This distribution’s pdf is the average of the inverse-Gaussian 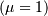 and reciprocal inverse-Gaussian pdf
and reciprocal inverse-Gaussian pdf 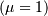 . We follow the notation of JKB here with
. We follow the notation of JKB here with 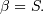 for
for 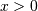
![\begin{eqnarray*} f\left(x;c\right) & = & \frac{x+1}{2c\sqrt{2\pi x^{3}}}\exp\left(-\frac{\left(x-1\right)^{2}}{2xc^{2}}\right)\\ F\left(x;c\right) & = & \Phi\left(\frac{1}{c}\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)\right)\\ G\left(q;c\right) & = & \frac{1}{4}\left[c\Phi^{-1}\left(q\right)+\sqrt{c^{2}\left(\Phi^{-1}\left(q\right)\right)^{2}+4}\right]^{2}\end{eqnarray*}](../../_images/math/07c67214c9fc56db0938fb52b8555c3284c9afe4.png)
![M\left(t\right)=c\sqrt{2\pi}\exp\left[\frac{1}{c^{2}}\left(1-\sqrt{1-2c^{2}t}\right)\right]\left(1+\frac{1}{\sqrt{1-2c^{2}t}}\right)](../../_images/math/e66f9b8ece3cb7e75126f7a76f287e6ad47a0784.png)
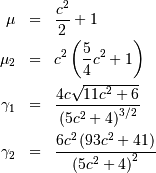
Folded Cauchy¶
This formula can be expressed in terms of the standard formulas for
the Cauchy distribution (call the cdf  and the pdf
and the pdf 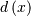 ). if
). if 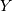 is cauchy then
is cauchy then 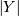 is folded cauchy. Note that
is folded cauchy. Note that 

No moments
Folded Normal¶
If 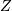 is Normal with mean
is Normal with mean 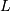 and
and 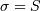 , then
, then 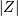 is a folded normal with shape parameter
is a folded normal with shape parameter 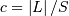 , location parameter
, location parameter 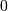 and scale parameter
and scale parameter 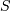 . This is a special case of the non-central chi distribution with one-
degree of freedom and non-centrality parameter
. This is a special case of the non-central chi distribution with one-
degree of freedom and non-centrality parameter 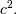 Note that
Note that 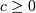 . The standard form of the folded normal is
. The standard form of the folded normal is
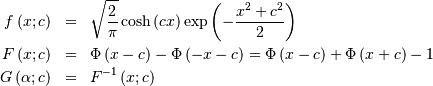
![M\left(t\right)=\exp\left[\frac{t}{2}\left(t-2c\right)\right]\left(1+e^{2ct}\right)](../../_images/math/e4009defedea34f04cfc810af9c93f2252607c38.png)
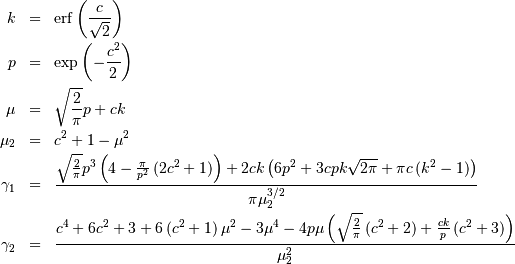
Fratio (or F)¶
Defined for 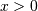 . The distribution of
. The distribution of 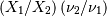 if
if  is chi-squared with
is chi-squared with 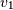 degrees of freedom and
degrees of freedom and 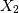 is chi-squared with
is chi-squared with  degrees of freedom.
degrees of freedom.
![\begin{eqnarray*} f\left(x;\nu_{1},\nu_{2}\right) & = & \frac{\nu_{2}^{\nu_{2}/2}\nu_{1}^{\nu_{1}/2}x^{\nu_{1}/2-1}}{\left(\nu_{2}+\nu_{1}x\right)^{\left(\nu_{1}+\nu_{2}\right)/2}B\left(\frac{\nu_{1}}{2},\frac{\nu_{2}}{2}\right)}\\ F\left(x;v_{1},v_{2}\right) & = & I\left(\frac{\nu_{1}}{2},\frac{\nu_{2}}{2},\frac{\nu_{2}x}{\nu_{2}+\nu_{1}x}\right)\\ G\left(q;\nu_{1},\nu_{2}\right) & = & \left[\frac{\nu_{2}}{I^{-1}\left(\nu_{1}/2,\nu_{2}/2,q\right)}-\frac{\nu_{1}}{\nu_{2}}\right]^{-1}.\end{eqnarray*}](../../_images/math/ac81267e83f8fffd3eea7ed766d8eaf0920a42a9.png)
![\begin{eqnarray*} \mu & = & \frac{\nu_{2}}{\nu_{2}-2}\quad\nu_{2}>2\\ \mu_{2} & = & \frac{2\nu_{2}^{2}\left(\nu_{1}+\nu_{2}-2\right)}{\nu_{1}\left(\nu_{2}-2\right)^{2}\left(\nu_{2}-4\right)}\quad v_{2}>4\\ \gamma_{1} & = & \frac{2\left(2\nu_{1}+\nu_{2}-2\right)}{\nu_{2}-6}\sqrt{\frac{2\left(\nu_{2}-4\right)}{\nu_{1}\left(\nu_{1}+\nu_{2}-2\right)}}\quad\nu_{2}>6\\ \gamma_{2} & = & \frac{3\left[8+\left(\nu_{2}-6\right)\gamma_{1}^{2}\right]}{2\nu-16}\quad\nu_{2}>8\end{eqnarray*}](../../_images/math/5954251798dcc50f83813c237d95cc435ea67e0a.png)
Fréchet (ExtremeLB, Extreme Value II, Weibull minimum)¶
A type of extreme-value distribution with a lower bound. Defined for 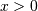 and
and 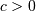
![\begin{eqnarray*} f\left(x;c\right) & = & cx^{c-1}\exp\left(-x^{c}\right)\\ F\left(x;c\right) & = & 1-\exp\left(-x^{c}\right)\\ G\left(q;c\right) & = & \left[-\log\left(1-q\right)\right]^{1/c}\end{eqnarray*}](../../_images/math/722c6c11d5a42c9e7471553f2167b6cd93cdce8d.png)

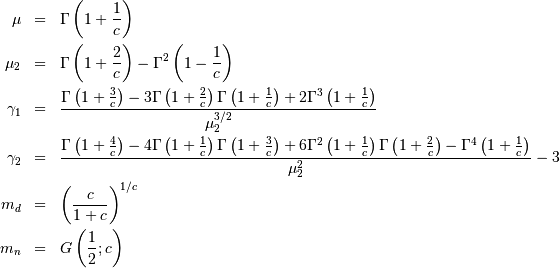
![h\left[X\right]=-\frac{\gamma}{c}-\log\left(c\right)+\gamma+1](../../_images/math/2a872f4c82170c8a86ae790bb331bf4a5f98f06c.png)
where  is Euler’s constant and equal to
is Euler’s constant and equal to
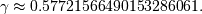
Fréchet (left-skewed, Extreme Value Type III, Weibull maximum)¶
Defined for 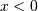 and
and 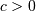 .
.
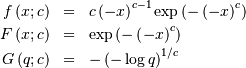
The mean is the negative of the right-skewed Frechet distribution given above, and the other statistical parameters can be computed from
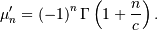
![h\left[X\right]=-\frac{\gamma}{c}-\log\left(c\right)+\gamma+1](../../_images/math/2a872f4c82170c8a86ae790bb331bf4a5f98f06c.png)
where  is Euler’s constant and equal to
is Euler’s constant and equal to
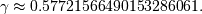
Generalized Logistic¶
Has been used in the analysis of extreme values. Has one shape
parameter 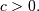 And
And 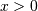
![\begin{eqnarray*} f\left(x;c\right) & = & \frac{c\exp\left(-x\right)}{\left[1+\exp\left(-x\right)\right]^{c+1}}\\ F\left(x;c\right) & = & \frac{1}{\left[1+\exp\left(-x\right)\right]^{c}}\\ G\left(q;c\right) & = & -\log\left(q^{-1/c}-1\right)\end{eqnarray*}](../../_images/math/0c46da5368838329abcff670edde935564f329cb.png)

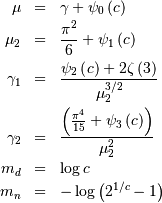
Note that the polygamma function is
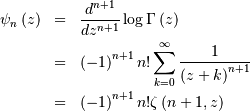
where 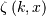 is a generalization of the Riemann zeta function called the Hurwitz
zeta function Note that
is a generalization of the Riemann zeta function called the Hurwitz
zeta function Note that 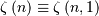
Generalized Extreme Value¶
Extreme value distributions with shape parameter  .
.
For 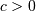 defined on
defined on 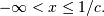
![\begin{eqnarray*} f\left(x;c\right) & = & \exp\left[-\left(1-cx\right)^{1/c}\right]\left(1-cx\right)^{1/c-1}\\ F\left(x;c\right) & = & \exp\left[-\left(1-cx\right)^{1/c}\right]\\ G\left(q;c\right) & = & \frac{1}{c}\left[1-\left(-\log q\right)^{c}\right]\end{eqnarray*}](../../_images/math/009c664acb3a59acc1d8d3f8772543b923fe90bd.png)
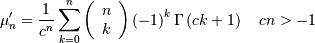
So,
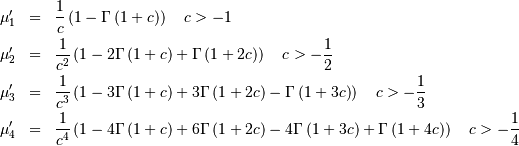
For 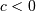 defined on
defined on 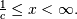 For
For 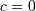 defined over all space
defined over all space
![\begin{eqnarray*} f\left(x;0\right) & = & \exp\left[-e^{-x}\right]e^{-x}\\ F\left(x;0\right) & = & \exp\left[-e^{-x}\right]\\ G\left(q;0\right) & = & -\log\left(-\log q\right)\end{eqnarray*}](../../_images/math/8b27682ea803fbeb9c2a048ab64bbd066ff4b198.png)
This is just the (left-skewed) Gumbel distribution for c=0.

Generalized Gamma¶
A general probability form that reduces to many common distributions: 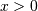
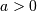 and
and 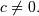
![\begin{eqnarray*} f\left(x;a,c\right) & = & \frac{\left|c\right|x^{ca-1}}{\Gamma\left(a\right)}\exp\left(-x^{c}\right)\\ F\left(x;a,c\right) & = & \begin{array}{cc} \frac{\Gamma\left(a,x^{c}\right)}{\Gamma\left(a\right)} & c>0\\ 1-\frac{\Gamma\left(a,x^{c}\right)}{\Gamma\left(a\right)} & c<0\end{array}\\ G\left(q;a,c\right) & = & \left\{ \Gamma^{-1}\left[a,\Gamma\left(a\right)q\right]\right\} ^{1/c}\quad c>0\\ & & \left\{ \Gamma^{-1}\left[a,\Gamma\left(a\right)\left(1-q\right)\right]\right\} ^{1/c}\quad c<0\end{eqnarray*}](../../_images/math/aee6c48c340829b855e5c3ea5dceab739e9921f2.png)
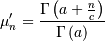
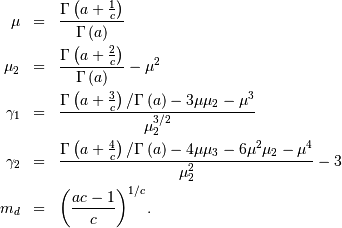
Special cases are Weibull  , half-normal
, half-normal 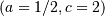 and ordinary gamma distributions
and ordinary gamma distributions 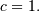 If
If 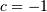 then it is the inverted gamma distribution.
then it is the inverted gamma distribution.
![h\left[X\right]=a-a\Psi\left(a\right)+\frac{1}{c}\Psi\left(a\right)+\log\Gamma\left(a\right)-\log\left|c\right|.](../../_images/math/57691c869dcffc54f2a40d23b62c24e502b6b94d.png)
Gompertz (Truncated Gumbel)¶
For 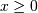 and
and 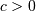 . In JKB the two shape parameters
. In JKB the two shape parameters  are reduced to the single shape-parameter
are reduced to the single shape-parameter 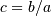 . As
. As  is just a scale parameter when
is just a scale parameter when 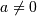 . If
. If 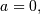 the distribution reduces to the exponential distribution scaled by
the distribution reduces to the exponential distribution scaled by 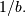 Thus, the standard form is given as
Thus, the standard form is given as
![\begin{eqnarray*} f\left(x;c\right) & = & ce^{x}\exp\left[-c\left(e^{x}-1\right)\right]\\ F\left(x;c\right) & = & 1-\exp\left[-c\left(e^{x}-1\right)\right]\\ G\left(q;c\right) & = & \log\left[1-\frac{1}{c}\log\left(1-q\right)\right]\end{eqnarray*}](../../_images/math/5b5851cfe541bfd0ded89b99103e4ffd76a4597b.png)
![h\left[X\right]=1-\log\left(c\right)-e^{c}\mathrm{Ei}\left(1,c\right),](../../_images/math/9b4f412fdc9f852b182092b73fa834029d403df4.png)
where
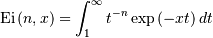
Gumbel (LogWeibull, Fisher-Tippetts, Type I Extreme Value)¶
One of a clase of extreme value distributions (right-skewed).
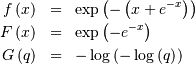
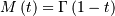

![h\left[X\right]\approx1.0608407169541684911](../../_images/math/98e2c047b9615f3c2e1c0e0ae453ca55e7aaf08e.png)
Gumbel Left-skewed (for minimum order statistic)¶
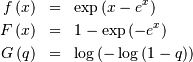
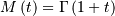
Note, that 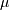 is negative the mean for the right-skewed distribution. Similar for
median and mode. All other moments are the same.
is negative the mean for the right-skewed distribution. Similar for
median and mode. All other moments are the same.
![h\left[X\right]\approx1.0608407169541684911.](../../_images/math/517847bcdbf6fc75f36ed586135800aba24139b2.png)
HalfCauchy¶
If 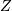 is Hyperbolic Secant distributed then
is Hyperbolic Secant distributed then 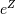 is Half-Cauchy distributed. Also, if
is Half-Cauchy distributed. Also, if 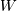 is (standard) Cauchy distributed, then
is (standard) Cauchy distributed, then 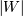 is Half-Cauchy distributed. Special case of the Folded Cauchy
distribution with
is Half-Cauchy distributed. Special case of the Folded Cauchy
distribution with 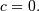 The standard form is
The standard form is
![\begin{eqnarray*} f\left(x\right) & = & \frac{2}{\pi\left(1+x^{2}\right)}I_{[0,\infty)}\left(x\right)\\ F\left(x\right) & = & \frac{2}{\pi}\arctan\left(x\right)I_{\left[0,\infty\right]}\left(x\right)\\ G\left(q\right) & = & \tan\left(\frac{\pi}{2}q\right)\end{eqnarray*}](../../_images/math/c330ff1dc0fe1f3887bf3beb01fb3e129f27e776.png)
![M\left(t\right)=\cos t+\frac{2}{\pi}\left[\mathrm{Si}\left(t\right)\cos t-\mathrm{Ci}\left(\mathrm{-}t\right)\sin t\right]](../../_images/math/d759e98997f9dcf4b0cae3c87764797058808300.png)

No moments, as the integrals diverge.
![\begin{eqnarray*} h\left[X\right] & = & \log\left(2\pi\right)\\ & \approx & 1.8378770664093454836.\end{eqnarray*}](../../_images/math/58856740f5f773861f4e6f7eab032a1d083158ef.png)
HalfNormal¶
This is a special case of the chi distribution with 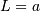 and
and 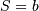 and
and 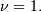 This is also a special case of the folded normal with shape parameter
This is also a special case of the folded normal with shape parameter 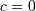 and
and  If
If 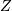 is (standard) normally distributed then,
is (standard) normally distributed then, 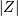 is half-normal. The standard form is
is half-normal. The standard form is
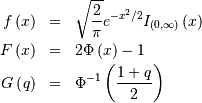
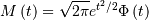

![\begin{eqnarray*} h\left[X\right] & = & \log\left(\sqrt{\frac{\pi e}{2}}\right)\\ & \approx & 0.72579135264472743239.\end{eqnarray*}](../../_images/math/829116d644e6ebbe42f2027e3f0dd9b0622b5dcf.png)
Half-Logistic¶
In the limit as 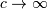 for the generalized half-logistic we have the half-logistic defined
over
for the generalized half-logistic we have the half-logistic defined
over  Also, the distribution of
Also, the distribution of 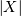 where
where 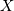 has logistic distribtution.
has logistic distribtution.
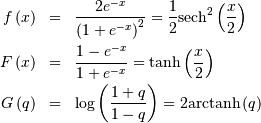
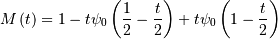

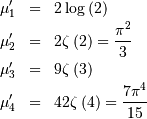
![\begin{eqnarray*} h\left[X\right] & = & 2-\log\left(2\right)\\ & \approx & 1.3068528194400546906.\end{eqnarray*}](../../_images/math/43b061aaf359455060f8d0f552e9203d4a1837cd.png)
Hyperbolic Secant¶
Related to the logistic distribution and used in lifetime analysis.
Standard form is (defined over all  )
)
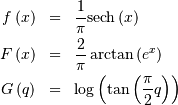

![\begin{eqnarray*} \mu_{n}^{\prime} & = & \frac{1+\left(-1\right)^{n}}{2\pi2^{2n}}n!\left[\zeta\left(n+1,\frac{1}{4}\right)-\zeta\left(n+1,\frac{3}{4}\right)\right]\\ & = & \left\{ \begin{array}{cc} 0 & n\mathrm{ odd}\\ C_{n/2}\frac{\pi^{n}}{2^{n}} & n\mathrm{ even}\end{array}\right.\end{eqnarray*}](../../_images/math/950df4d3140c73363970c9a52792015e90571842.png)
where  is an integer given by
is an integer given by
![\begin{eqnarray*} C_{m} & = & \frac{\left(2m\right)!\left[\zeta\left(2m+1,\frac{1}{4}\right)-\zeta\left(2m+1,\frac{3}{4}\right)\right]}{\pi^{2m+1}2^{2m}}\\ & = & 4\left(-1\right)^{m-1}\frac{16^{m}}{2m+1}B_{2m+1}\left(\frac{1}{4}\right)\end{eqnarray*}](../../_images/math/913c4a7db7db50fa6cb8823b24ea6eb8e0a6a628.png)
where 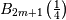 is the Bernoulli polynomial of order
is the Bernoulli polynomial of order 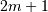 evaluated at
evaluated at 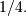 Thus
Thus
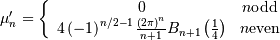
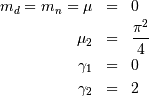
![h\left[X\right]=\log\left(2\pi\right).](../../_images/math/1d3f67fcda9b9b528886c74a81921305e70b9d9f.png)
Inverse Normal (Inverse Gaussian)¶
The standard form involves the shape parameter 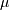 (in most definitions,
(in most definitions, 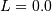 is used). (In terms of the regress documentation
is used). (In terms of the regress documentation 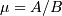 ) and
) and 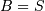 and
and 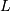 is not a parameter in that distribution. A standard form is
is not a parameter in that distribution. A standard form is 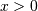
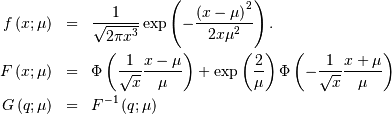
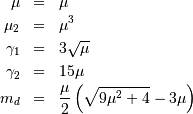
This is related to the canonical form or JKB “two-parameter “inverse Gaussian when written in it’s full form with scale parameter 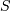 and location parameter
and location parameter 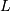 by taking
by taking 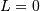 and
and 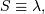 then
then 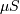 is equal to
is equal to 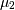 where
where 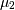 is the parameter used by JKB. We prefer this form because of it’s
consistent use of the scale parameter. Notice that in JKB the skew
is the parameter used by JKB. We prefer this form because of it’s
consistent use of the scale parameter. Notice that in JKB the skew 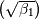 and the kurtosis (
and the kurtosis ( 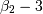 ) are both functions only of
) are both functions only of 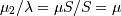 as shown here, while the variance and mean of the standard form here
are transformed appropriately.
as shown here, while the variance and mean of the standard form here
are transformed appropriately.
KSone¶
KStwo¶
Laplace (Double Exponential, Bilateral Expoooonential)¶


The ML estimator of the location parameter is
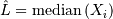
where 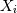 is a sequence of
is a sequence of 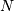 mutually independent Laplace RV’s and the median is some number
between the
mutually independent Laplace RV’s and the median is some number
between the 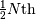 and the
and the 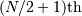 order statistic ( e.g. take the average of these two) when
order statistic ( e.g. take the average of these two) when 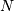 is even. Also,
is even. Also,
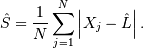
Replace 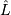 with
with 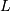 if it is known. If
if it is known. If 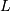 is known then this estimator is distributed as
is known then this estimator is distributed as 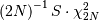 .
.
![\begin{eqnarray*} h\left[X\right] & = & \log\left(2e\right)\\ & \approx & 1.6931471805599453094.\end{eqnarray*}](../../_images/math/d78521a2281dc12e74c0e711252585699d7a70f4.png)
Left-skewed Lévy¶
Special case of Lévy-stable distribution with 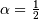 and
and  the support is
the support is 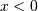 . In standard form
. In standard form
![\begin{eqnarray*} f\left(x\right) & = & \frac{1}{\left|x\right|\sqrt{2\pi\left|x\right|}}\exp\left(-\frac{1}{2\left|x\right|}\right)\\ F\left(x\right) & = & 2\Phi\left(\frac{1}{\sqrt{\left|x\right|}}\right)-1\\ G\left(q\right) & = & -\left[\Phi^{-1}\left(\frac{q+1}{2}\right)\right]^{-2}.\end{eqnarray*}](../../_images/math/b1c62d78e007b20f0ed46f9bd4c7dfdc144c9efc.png)
No moments.
Lévy¶
A special case of Lévy-stable distributions with 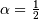 and
and 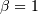 . In standard form it is defined for
. In standard form it is defined for 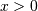 as
as
![\begin{eqnarray*} f\left(x\right) & = & \frac{1}{x\sqrt{2\pi x}}\exp\left(-\frac{1}{2x}\right)\\ F\left(x\right) & = & 2\left[1-\Phi\left(\frac{1}{\sqrt{x}}\right)\right]\\ G\left(q\right) & = & \left[\Phi^{-1}\left(1-\frac{q}{2}\right)\right]^{-2}.\end{eqnarray*}](../../_images/math/12966cf5cf4884342a0b54a5311bdd6b3d08cbe7.png)
It has no finite moments.
Log Normal (Cobb-Douglass)¶
Has one shape parameter  >0. (Notice that the “Regress “
>0. (Notice that the “Regress “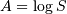 where
where 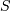 is the scale parameter and
is the scale parameter and 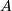 is the mean of the underlying normal distribution). The standard form
is
is the mean of the underlying normal distribution). The standard form
is 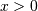
![\begin{eqnarray*} f\left(x;\sigma\right) & = & \frac{1}{\sigma x\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{\log x}{\sigma}\right)^{2}\right]\\ F\left(x;\sigma\right) & = & \Phi\left(\frac{\log x}{\sigma}\right)\\ G\left(q;\sigma\right) & = & \exp\left\{ \sigma\Phi^{-1}\left(q\right)\right\} \end{eqnarray*}](../../_images/math/b601bf6d5043714b48b85865511972fcc921b7ee.png)
![\begin{eqnarray*} \mu & = & \exp\left(\sigma^{2}/2\right)\\ \mu_{2} & = & \exp\left(\sigma^{2}\right)\left[\exp\left(\sigma^{2}\right)-1\right]\\ \gamma_{1} & = & \sqrt{p-1}\left(2+p\right)\\ \gamma_{2} & = & p^{4}+2p^{3}+3p^{2}-6\quad\quad p=e^{\sigma^{2}}\end{eqnarray*}](../../_images/math/7c101da5174583b330c87d8556cff81721bb51ea.png)
Notice that using JKB notation we have 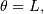
 and we have given the so-called antilognormal form of the
distribution. This is more consistent with the location, scale
parameter description of general probability distributions.
and we have given the so-called antilognormal form of the
distribution. This is more consistent with the location, scale
parameter description of general probability distributions.
![h\left[X\right]=\frac{1}{2}\left[1+\log\left(2\pi\right)+2\log\left(\sigma\right)\right].](../../_images/math/0216fb71fdda9e373eda893afb73a9e5e0ebfbb2.png)
Also, note that if 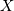 is a log-normally distributed random-variable with
is a log-normally distributed random-variable with 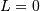 and
and 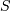 and shape parameter
and shape parameter 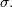 Then,
Then,  is normally distributed with variance
is normally distributed with variance 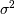 and mean
and mean 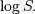
Noncentral chi*¶
Noncentral chi-squared¶
The distribution of 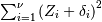 where
where  are independent standard normal variables and
are independent standard normal variables and  are constants.
are constants. 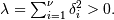 (In communications it is called the Marcum-Q function). Can be thought
of as a Generalized Rayleigh-Rice distribution. For
(In communications it is called the Marcum-Q function). Can be thought
of as a Generalized Rayleigh-Rice distribution. For 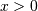
![\begin{eqnarray*} f\left(x;\nu,\lambda\right) & = & e^{-\left(\lambda+x\right)/2}\frac{1}{2}\left(\frac{x}{\lambda}\right)^{\left(\nu-2\right)/4}I_{\left(\nu-2\right)/2}\left(\sqrt{\lambda x}\right)\\ F\left(x;\nu,\lambda\right) & = & \sum_{j=0}^{\infty}\left\{ \frac{\left(\lambda/2\right)^{j}}{j!}e^{-\lambda/2}\right\} \mathrm{Pr}\left[\chi_{\nu+2j}^{2}\leq x\right]\\ G\left(q;\nu,\lambda\right) & = & F^{-1}\left(x;\nu,\lambda\right)\end{eqnarray*}](../../_images/math/79f8b1fb02f885dd8e6e9bb67d8e756d5c8868f0.png)

Noncentral t¶
The distribution of the ratio
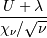
where 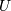 and
and 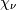 are independent and distributed as a standard normal and chi with
are independent and distributed as a standard normal and chi with  degrees of freedom. Note
degrees of freedom. Note  and
and 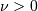 .
.
![\begin{eqnarray*} f\left(x;\lambda,\nu\right) & = & \frac{\nu^{\nu/2}\Gamma\left(\nu+1\right)}{2^{\nu}e^{\lambda^{2}/2}\left(\nu+x^{2}\right)^{\nu/2}\Gamma\left(\nu/2\right)}\\ & & \times\left\{ \frac{\sqrt{2}\lambda x\,_{1}F_{1}\left(\frac{\nu}{2}+1;\frac{3}{2};\frac{\lambda^{2}x^{2}}{2\left(\nu+x^{2}\right)}\right)}{\left(\nu+x^{2}\right)\Gamma\left(\frac{\nu+1}{2}\right)}\right.\\ & & -\left.\frac{\,_{1}F_{1}\left(\frac{\nu+1}{2};\frac{1}{2};\frac{\lambda^{2}x^{2}}{2\left(\nu+x^{2}\right)}\right)}{\sqrt{\nu+x^{2}}\Gamma\left(\frac{\nu}{2}+1\right)}\right\} \\ & = & \frac{\Gamma\left(\nu+1\right)}{2^{\left(\nu-1\right)/2}\sqrt{\pi\nu}\Gamma\left(\nu/2\right)}\exp\left[-\frac{\nu\lambda^{2}}{\nu+x^{2}}\right]\\ & & \times\left(\frac{\nu}{\nu+x^{2}}\right)^{\left(\nu-1\right)/2}Hh_{\nu}\left(-\frac{\lambda x}{\sqrt{\nu+x^{2}}}\right)\\ F\left(x;\lambda,\nu\right) & =\end{eqnarray*}](../../_images/math/29b73b069323987158cb3caec94f3dfffa85195f.png)
Mielke’s Beta-Kappa¶
A generalized F distribution. Two shape parameters  and
and 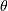 , and
, and 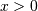 . The
. The 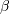 in the DATAPLOT reference is a scale parameter.
in the DATAPLOT reference is a scale parameter.

Power Log Normal¶
A generalization of the log-normal distribution  and
and 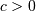 and
and 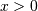
![\begin{eqnarray*} f\left(x;\sigma,c\right) & = & \frac{c}{x\sigma}\phi\left(\frac{\log x}{\sigma}\right)\left(\Phi\left(-\frac{\log x}{\sigma}\right)\right)^{c-1}\\ F\left(x;\sigma,c\right) & = & 1-\left(\Phi\left(-\frac{\log x}{\sigma}\right)\right)^{c}\\ G\left(q;\sigma,c\right) & = & \exp\left[-\sigma\Phi^{-1}\left[\left(1-q\right)^{1/c}\right]\right]\end{eqnarray*}](../../_images/math/f9039f8e8762e4fb6ae0175fcaf5d2dd69e676a9.png)
![\mu_{n}^{\prime}=\int_{0}^{1}\exp\left[-n\sigma\Phi^{-1}\left(y^{1/c}\right)\right]dy](../../_images/math/6b846f38192715dbf43007b6f2082999e67e1ff3.png)
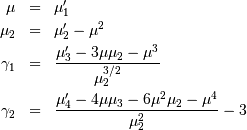
This distribution reduces to the log-normal distribution when 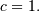
Power Normal¶
A generalization of the normal distribution, 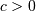 for
for
![\begin{eqnarray*} f\left(x;c\right) & = & c\phi\left(x\right)\left(\Phi\left(-x\right)\right)^{c-1}\\ F\left(x;c\right) & = & 1-\left(\Phi\left(-x\right)\right)^{c}\\ G\left(q;c\right) & = & -\Phi^{-1}\left[\left(1-q\right)^{1/c}\right]\end{eqnarray*}](../../_images/math/957af35703572e5d8ed7d32aab2d64b9a05d2480.png)
![\mu_{n}^{\prime}=\left(-1\right)^{n}\int_{0}^{1}\left[\Phi^{-1}\left(y^{1/c}\right)\right]^{n}dy](../../_images/math/085e6bd52fb951396c14d5843b2c546154158b38.png)
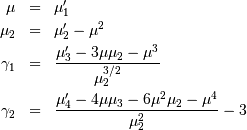
For  this reduces to the normal distribution.
this reduces to the normal distribution.
R-distribution¶
A general-purpose distribution with a variety of shapes controlled by 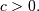 Range of standard distribution is
Range of standard distribution is ![x\in\left[-1,1\right]](../../_images/math/5367b84b936165ca9fffdc5ee9383c08a19a6374.png)
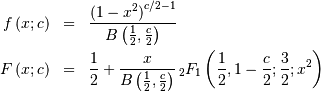
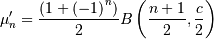
The R-distribution with parameter  is the distribution of the correlation coefficient of a random sample
of size
is the distribution of the correlation coefficient of a random sample
of size  drawn from a bivariate normal distribution with
drawn from a bivariate normal distribution with 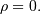 The mean of the standard distribution is always zero and as the sample
size grows, the distribution’s mass concentrates more closely about
this mean.
The mean of the standard distribution is always zero and as the sample
size grows, the distribution’s mass concentrates more closely about
this mean.
Rayleigh¶
This is Chi distribution with 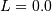 and
and 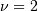 and
and  (no location parameter is generally used), the mode of the
distribution is
(no location parameter is generally used), the mode of the
distribution is 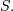
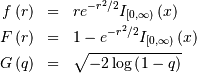
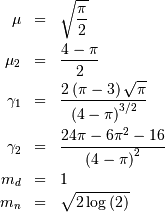
![h\left[X\right]=\frac{\gamma}{2}+\log\left(\frac{e}{\sqrt{2}}\right).](../../_images/math/621271974672ea33a764bb852c1e3708bff23fe6.png)
Studentized Range*¶
Student t¶
Shape parameter 
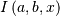 is the incomplete beta integral and
is the incomplete beta integral and 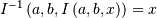
![\begin{eqnarray*} f\left(x;\nu\right) & = & \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\pi\nu}\Gamma\left(\frac{\nu}{2}\right)\left[1+\frac{x^{2}}{\nu}\right]^{\frac{\nu+1}{2}}}\\ F\left(x;\nu\right) & = & \left\{ \begin{array}{ccc} \frac{1}{2}I\left(\frac{\nu}{2},\frac{1}{2},\frac{\nu}{\nu+x^{2}}\right) & & x\leq0\\ 1-\frac{1}{2}I\left(\frac{\nu}{2},\frac{1}{2},\frac{\nu}{\nu+x^{2}}\right) & & x\geq0\end{array}\right.\\ G\left(q;\nu\right) & = & \left\{ \begin{array}{ccc} -\sqrt{\frac{\nu}{I^{-1}\left(\frac{\nu}{2},\frac{1}{2},2q\right)}-\nu} & & q\leq\frac{1}{2}\\ \sqrt{\frac{\nu}{I^{-1}\left(\frac{\nu}{2},\frac{1}{2},2-2q\right)}-\nu} & & q\geq\frac{1}{2}\end{array}\right.\end{eqnarray*}](../../_images/math/cdbbc82838e1a05be55105d1bf591dad4f96616d.png)
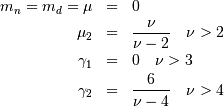
As 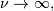 this distribution approaches the standard normal distribution.
this distribution approaches the standard normal distribution.
![h\left[X\right]=\frac{1}{4}\log\left(\frac{\pi c\Gamma^{2}\left(\frac{c}{2}\right)}{\Gamma^{2}\left(\frac{c+1}{2}\right)}\right)-\frac{\left(c+1\right)}{4}\left[\Psi\left(\frac{c}{2}\right)-cZ\left(c\right)+\pi\tan\left(\frac{\pi c}{2}\right)+\gamma+2\log2\right]](../../_images/math/b71d9b8aa5966222fb404a0b74086b4a36470862.png)
where
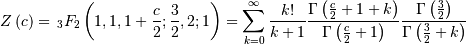
Student Z¶
The student Z distriubtion is defined over all space with one shape
parameter 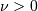
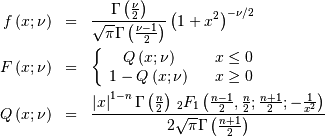
Interesting moments are
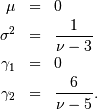
The moment generating function is
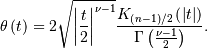
Symmetric Power*¶
Triangular¶
One shape parameter ![c\in[0,1]](../../_images/math/3e17bb1ebb283a54aac6c753fb6ec8d6a7e6df98.png) giving the distance to the peak as a percentage of the total extent of
the non-zero portion. The location parameter is the start of the non-
zero portion, and the scale-parameter is the width of the non-zero
portion. In standard form we have
giving the distance to the peak as a percentage of the total extent of
the non-zero portion. The location parameter is the start of the non-
zero portion, and the scale-parameter is the width of the non-zero
portion. In standard form we have ![x\in\left[0,1\right].](../../_images/math/bdc93d1147f2643dcc726495e47594043a3f3f64.png)
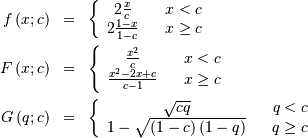
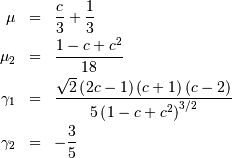
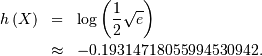
Truncated Exponential¶
This is an exponential distribution defined only over a certain region 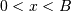 . In standard form this is
. In standard form this is
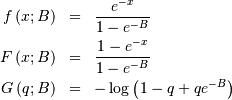

![h\left[X\right]=\log\left(e^{B}-1\right)+\frac{1+e^{B}\left(B-1\right)}{1-e^{B}}.](../../_images/math/323abedcee36218c9abe947b0c48e9d1a363fe6b.png)
Truncated Normal¶
A normal distribution restricted to lie within a certain range given
by two parameters 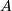 and
and 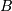 . Notice that this
. Notice that this 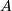 and
and 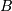 correspond to the bounds on
correspond to the bounds on  in standard form. For
in standard form. For ![x\in\left[A,B\right]](../../_images/math/72fc9fcb7d13970d5529596da450cb50e222568a.png) we get
we get
![\begin{eqnarray*} f\left(x;A,B\right) & = & \frac{\phi\left(x\right)}{\Phi\left(B\right)-\Phi\left(A\right)}\\ F\left(x;A,B\right) & = & \frac{\Phi\left(x\right)-\Phi\left(A\right)}{\Phi\left(B\right)-\Phi\left(A\right)}\\ G\left(q;A,B\right) & = & \Phi^{-1}\left[q\Phi\left(B\right)+\Phi\left(A\right)\left(1-q\right)\right]\end{eqnarray*}](../../_images/math/fd7b7a7944b86b192e53254f6cd31b57b90b3d77.png)
where
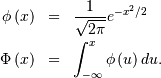
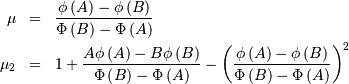
Von Mises¶
Defined for ![x\in\left[-\pi,\pi\right]](../../_images/math/a1458a505dea3f7eee8d4bf76e2e67e428f7b6f6.png) with shape parameter
with shape parameter 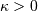 . Note, the PDF and CDF functions are periodic and are always defined
over
. Note, the PDF and CDF functions are periodic and are always defined
over ![x\in\left[-\pi,\pi\right]](../../_images/math/a1458a505dea3f7eee8d4bf76e2e67e428f7b6f6.png) regardless of the location parameter. Thus, if an input beyond this
range is given, it is converted to the equivalent angle in this range.
For values of
regardless of the location parameter. Thus, if an input beyond this
range is given, it is converted to the equivalent angle in this range.
For values of 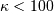 the PDF and CDF formulas below are used. Otherwise, a normal
approximation with variance
the PDF and CDF formulas below are used. Otherwise, a normal
approximation with variance 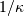 is used.
is used.
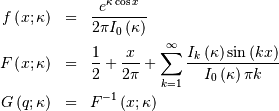
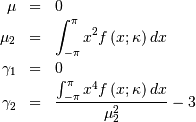
This can be used for defining circular variance.

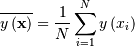
![x\in\left[-\frac{\pi}{4},\frac{\pi}{4}\right]](../../_images/math/370e739556faafc05399ad3b9f88321c226edaac.png)
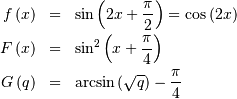

![\begin{eqnarray*} h\left[X\right] & = & 1-\log2\\ & \approx & 0.30685281944005469058\end{eqnarray*}](../../_images/math/7e9530b0a8dbaf1a8145c789b0fb37d95ea5768f.png)

![l_{\mathbf{x}}\left(\cdot\right)=-N\overline{\log\left[\cos\left(2\mathbf{x}\right)\right]}](../../_images/math/cd23b55ed7a4cc6a1220f5f57bfd09d1dedb5ad3.png)
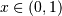 . To get the JKB definition put
. To get the JKB definition put 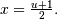 i.e.
i.e. 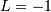 and
and 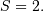
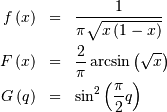
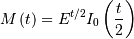
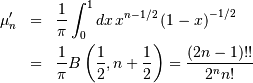

![h\left[X\right]\approx-0.24156447527049044468](../../_images/math/0c7fc236a334e37b52f3f0c5d4a02672959d910a.png)
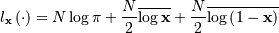

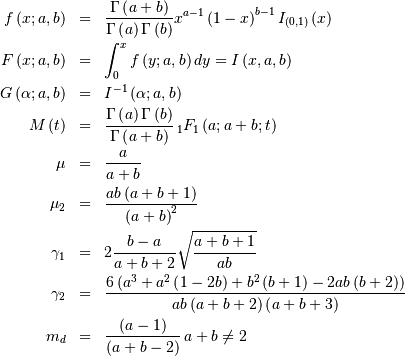
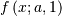 is also called the Power-function distribution.
is also called the Power-function distribution.
![x_{i}\in\left[0,1\right]](../../_images/math/9bdfd4256caed79ee5be6d2293848da3fea6ab5c.png)
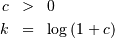
![\begin{eqnarray*} f\left(x;c\right) & = & \frac{c}{k\left(1+cx\right)}I_{\left(0,1\right)}\left(x\right)\\ F\left(x;c\right) & = & \frac{\log\left(1+cx\right)}{k}\\ G\left(\alpha\; c\right) & = & \frac{\left(1+c\right)^{\alpha}-1}{c}\\ M\left(t\right) & = & \frac{1}{k}e^{-t/c}\left[\mathrm{Ei}\left(t+\frac{t}{c}\right)-\mathrm{Ei}\left(\frac{t}{c}\right)\right]\\ \mu & = & \frac{c-k}{ck}\\ \mu_{2} & = & \frac{\left(c+2\right)k-2c}{2ck^{2}}\\ \gamma_{1} & = & \frac{\sqrt{2}\left(12c^{2}-9kc\left(c+2\right)+2k^{2}\left(c\left(c+3\right)+3\right)\right)}{\sqrt{c\left(c\left(k-2\right)+2k\right)}\left(3c\left(k-2\right)+6k\right)}\\ \gamma_{2} & = & \frac{c^{3}\left(k-3\right)\left(k\left(3k-16\right)+24\right)+12kc^{2}\left(k-4\right)\left(k-3\right)+6ck^{2}\left(3k-14\right)+12k^{3}}{3c\left(c\left(k-2\right)+2k\right)^{2}}\\ m_{d} & = & 0\\ m_{n} & = & \sqrt{1+c}-1\end{eqnarray*}](../../_images/math/cfd44935d35ff2bb3759d72828ac8f3f523e7fde.png)
 is the exponential integral function. Also
is the exponential integral function. Also![h\left[X\right]=\frac{1}{2}\log\left(1+c\right)-\log\left(\frac{c}{\log\left(1+c\right)}\right)](../../_images/math/3fabf3e44b10b949cd45056ecee41960d9d6deaf.png)
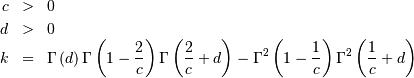
![\begin{eqnarray*} f\left(x;c,d\right) & = & \frac{cd}{x^{c+1}\left(1+x^{-c}\right)^{d+1}}I_{\left(0,\infty\right)}\left(x\right)\\ F\left(x;c,d\right) & = & \left(1+x^{-c}\right)^{-d}\\ G\left(\alpha;c,d\right) & = & \left(\alpha^{-1/d}-1\right)^{-1/c}\\ \mu & = & \frac{\Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+d\right)}{\Gamma\left(d\right)}\\ \mu_{2} & = & \frac{k}{\Gamma^{2}\left(d\right)}\\ \gamma_{1} & = & \frac{1}{\sqrt{k^{3}}}\left[2\Gamma^{3}\left(1-\frac{1}{c}\right)\Gamma^{3}\left(\frac{1}{c}+d\right)+\Gamma^{2}\left(d\right)\Gamma\left(1-\frac{3}{c}\right)\Gamma\left(\frac{3}{c}+d\right)\right.\\ & & \left.-3\Gamma\left(d\right)\Gamma\left(1-\frac{2}{c}\right)\Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+d\right)\Gamma\left(\frac{2}{c}+d\right)\right]\\ \gamma_{2} & = & -3+\frac{1}{k^{2}}\left[6\Gamma\left(d\right)\Gamma\left(1-\frac{2}{c}\right)\Gamma^{2}\left(1-\frac{1}{c}\right)\Gamma^{2}\left(\frac{1}{c}+d\right)\Gamma\left(\frac{2}{c}+d\right)\right.\\ & & -3\Gamma^{4}\left(1-\frac{1}{c}\right)\Gamma^{4}\left(\frac{1}{c}+d\right)+\Gamma^{3}\left(d\right)\Gamma\left(1-\frac{4}{c}\right)\Gamma\left(\frac{4}{c}+d\right)\\ & & \left.-4\Gamma^{2}\left(d\right)\Gamma\left(1-\frac{3}{c}\right)\Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+d\right)\Gamma\left(\frac{3}{c}+d\right)\right]\\ m_{d} & = & \left(\frac{cd-1}{c+1}\right)^{1/c}\,\mathrm{if }cd>1\,\mathrm{otherwise }0\\ m_{n} & = & \left(2^{1/d}-1\right)^{-1/c}\end{eqnarray*}](../../_images/math/89c5855f4e0ccecd0e337dad8ff654dc48622ad3.png)
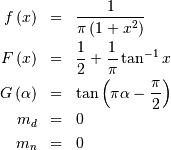
![\begin{eqnarray*} h\left[X\right] & = & \log\left(4\pi\right)\\ & \approx & 2.5310242469692907930.\end{eqnarray*}](../../_images/math/07bdd3f3b7b6ff7533ec6e61374799c6f99b2f0c.png)
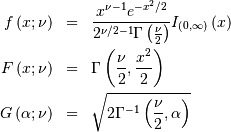

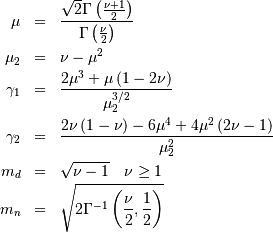
![\begin{eqnarray*} f\left(x\right) & = & \frac{1}{2\pi}\left[1+\cos x\right]I_{\left[-\pi,\pi\right]}\left(x\right)\\ F\left(x\right) & = & \frac{1}{2\pi}\left[\pi+x+\sin x\right]I_{\left[-\pi,\pi\right]}\left(x\right)+I_{\left(\pi,\infty\right)}\left(x\right)\\ G\left(\alpha\right) & = & F^{-1}\left(\alpha\right)\\ M\left(t\right) & = & \frac{\sinh\left(\pi t\right)}{\pi t\left(1+t^{2}\right)}\\ \mu=m_{d}=m_{n} & = & 0\\ \mu_{2} & = & \frac{\pi^{2}}{3}-2\\ \gamma_{1} & = & 0\\ \gamma_{2} & = & \frac{-6\left(\pi^{4}-90\right)}{5\left(\pi^{2}-6\right)^{2}}\end{eqnarray*}](../../_images/math/a6b0767eec26ab74ef8345a49b7c1de4927a7961.png)
![\begin{eqnarray*} h\left[X\right] & = & \log\left(4\pi\right)-1\\ & \approx & 1.5310242469692907930.\end{eqnarray*}](../../_images/math/6635d56b76c8c54a28f103ef52ea743e1f72d17a.png)
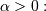
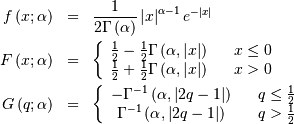
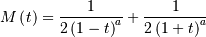
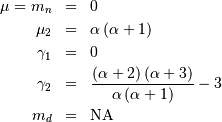
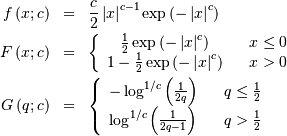
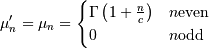
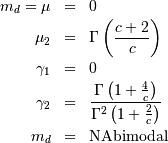
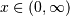
![\begin{eqnarray*} f\left(x;a,c\right) & = & ac\left[1-\exp\left(-x^{c}\right)\right]^{a-1}\exp\left(-x^{c}\right)x^{c-1}\\ F\left(x;a,c\right) & = & \left[1-\exp\left(-x^{c}\right)\right]^{a}\\ G\left(q;a,c\right) & = & \left[-\log\left(1-q^{1/a}\right)\right]^{1/c}\end{eqnarray*}](../../_images/math/9ee6b6560f0c09dd5b8f7d605581a9daaa572fcd.png)
 . Defined for
. Defined for ![\begin{eqnarray*} f\left(x;b\right) & = & ebx^{b-1}\exp\left[x^{b}-e^{x^{b}}\right]\\ F\left(x;b\right) & = & 1-\exp\left[1-e^{x^{b}}\right]\\ G\left(q;b\right) & = & \log^{1/b}\left[1-\log\left(1-q\right)\right]\end{eqnarray*}](../../_images/math/2baa47c4fabef686890a91182377520b010de360.png)
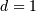
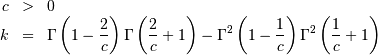
![\begin{eqnarray*} f\left(x;c,d\right) & = & \frac{cx^{c-1}}{\left(1+x^{c}\right)^{2}}I_{\left(0,\infty\right)}\left(x\right)\\ F\left(x;c,d\right) & = & \left(1+x^{-c}\right)^{-1}\\ G\left(\alpha;c,d\right) & = & \left(\alpha^{-1}-1\right)^{-1/c}\\ \mu & = & \Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+1\right)\\ \mu_{2} & = & k\\ \gamma_{1} & = & \frac{1}{\sqrt{k^{3}}}\left[2\Gamma^{3}\left(1-\frac{1}{c}\right)\Gamma^{3}\left(\frac{1}{c}+1\right)+\Gamma\left(1-\frac{3}{c}\right)\Gamma\left(\frac{3}{c}+1\right)\right.\\ & & \left.-3\Gamma\left(1-\frac{2}{c}\right)\Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+1\right)\Gamma\left(\frac{2}{c}+1\right)\right]\\ \gamma_{2} & = & -3+\frac{1}{k^{2}}\left[6\Gamma\left(1-\frac{2}{c}\right)\Gamma^{2}\left(1-\frac{1}{c}\right)\Gamma^{2}\left(\frac{1}{c}+1\right)\Gamma\left(\frac{2}{c}+1\right)\right.\\ & & -3\Gamma^{4}\left(1-\frac{1}{c}\right)\Gamma^{4}\left(\frac{1}{c}+1\right)+\Gamma\left(1-\frac{4}{c}\right)\Gamma\left(\frac{4}{c}+1\right)\\ & & \left.-4\Gamma\left(1-\frac{3}{c}\right)\Gamma\left(1-\frac{1}{c}\right)\Gamma\left(\frac{1}{c}+1\right)\Gamma\left(\frac{3}{c}+1\right)\right]\\ m_{d} & = & \left(\frac{c-1}{c+1}\right)^{1/c}\,\mathrm{if }c>1\,\mathrm{otherwise }0\\ m_{n} & = & 1\end{eqnarray*}](../../_images/math/6db0a7916d1038d7abc99a3e6c00fd5424a88d7c.png)
![h\left[X\right]=2-\log c.](../../_images/math/fd370b8ab44f92dc003db7ebf16914d91d678c4b.png)
 valid for
valid for 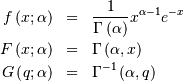


![h\left[X\right]=\Psi\left(a\right)\left[1-a\right]+a+\log\Gamma\left(a\right)](../../_images/math/ccb656ff8b9fe50f3be1c9f0113da0541af61fc3.png)
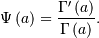
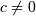 and defined for
and defined for 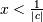 if
if ![\begin{eqnarray*} f\left(x;c\right) & = & \left(1+cx\right)^{-1-\frac{1}{c}}\\ F\left(x;c\right) & = & 1-\frac{1}{\left(1+cx\right)^{1/c}}\\ G\left(q;c\right) & = & \frac{1}{c}\left[\left(\frac{1}{1-q}\right)^{c}-1\right]\end{eqnarray*}](../../_images/math/e6b293d7f811cba54799ba8b0d661e802082492e.png)
![M\left(t\right)=\left\{ \begin{array}{cc} \left(-\frac{t}{c}\right)^{\frac{1}{c}}e^{-\frac{t}{c}}\left[\Gamma\left(1-\frac{1}{c}\right)+\Gamma\left(-\frac{1}{c},-\frac{t}{c}\right)-\pi\csc\left(\frac{\pi}{c}\right)/\Gamma\left(\frac{1}{c}\right)\right] & c>0\\ \left(\frac{\left|c\right|}{t}\right)^{1/\left|c\right|}\Gamma\left[\frac{1}{\left|c\right|},\frac{t}{\left|c\right|}\right] & c<0\end{array}\right.](../../_images/math/31af9d5bbbef6a175d3d40884c818979b5ce1d78.png)
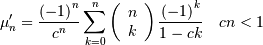
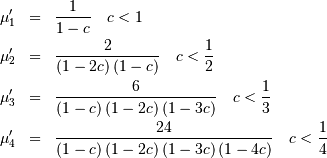
![h\left[X\right]=1+c\quad c>0](../../_images/math/f68023578f0fd730b455014ae5eac58a715c19ae.png)
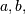 and
and 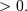
![\begin{eqnarray*} f\left(x;a,b,c\right) & = & \left(a+b\left(1-e^{-cx}\right)\right)\exp\left[ax-bx+\frac{b}{c}\left(1-e^{-cx}\right)\right]\\ F\left(x;a,b,c\right) & = & 1-\exp\left[ax-bx+\frac{b}{c}\left(1-e^{-cx}\right)\right]\\ G\left(q;a,b,c\right) & = & F^{-1}\end{eqnarray*}](../../_images/math/eaeb420a9b5de4886d1d2727fef677b237f3b566.png)
![x\in\left[0,1/c\right]](../../_images/math/386faa5a24925bc3bd80f271523915054b98db09.png) and
and ![\begin{eqnarray*} f\left(x;c\right) & = & \frac{2\left(1-cx\right)^{\frac{1}{c}-1}}{\left(1+\left(1-cx\right)^{1/c}\right)^{2}}\\ F\left(x;c\right) & = & \frac{1-\left(1-cx\right)^{1/c}}{1+\left(1-cx\right)^{1/c}}\\ G\left(q;c\right) & = & \frac{1}{c}\left[1-\left(\frac{1-q}{1+q}\right)^{c}\right]\end{eqnarray*}](../../_images/math/46a7c2a67cc5f3b196ac0481788fd3405dce13f9.png)
![\begin{eqnarray*} h\left[X\right] & = & 2-\left(2c+1\right)\log2.\end{eqnarray*}](../../_images/math/a3c630ded83ea3909afe6a4a9c8a7e511971abd2.png)
 and
and 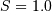 (typically also
(typically also ![\begin{eqnarray*} f\left(x;\sigma\right) & = & \frac{1}{x\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\log x\right)^{2}\right]\\ F\left(x;\sigma\right) & = & \Phi\left(\log x\right)=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{\log x}{\sqrt{2}}\right)\right]\\ G\left(q;\sigma\right) & = & \exp\left\{ \Phi^{-1}\left(q\right)\right\} \end{eqnarray*}](../../_images/math/a88acf36ca58bca157a9d34f538ac385cf6d7d07.png)
![\begin{eqnarray*} \mu & = & \sqrt{e}\\ \mu_{2} & = & e\left[e-1\right]\\ \gamma_{1} & = & \sqrt{e-1}\left(2+e\right)\\ \gamma_{2} & = & e^{4}+2e^{3}+3e^{2}-6\end{eqnarray*}](../../_images/math/b5173189ab21def369b55be2dcfe23f984786122.png)
![\begin{eqnarray*} h\left[X\right] & = & \log\left(\sqrt{2\pi e}\right)\\ & \approx & 1.4189385332046727418\end{eqnarray*}](../../_images/math/360522a83bdf6c8c4a075710897ee2f40b4a6ee4.png)
![x\in\left[0,1\right]](../../_images/math/77d287156fda15acf3439ce0326e8a9a9a4a3a84.png) ,
, 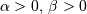
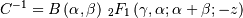
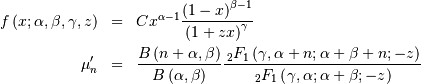
![\begin{eqnarray*} f\left(x;a\right) & = & \frac{x^{-a-1}}{\Gamma\left(a\right)}\exp\left(-\frac{1}{x}\right)\\ F\left(x;a\right) & = & \frac{\Gamma\left(a,\frac{1}{x}\right)}{\Gamma\left(a\right)}\\ G\left(q;a\right) & = & \left\{ \Gamma^{-1}\left[a,\Gamma\left(a\right)q\right]\right\} ^{-1}\end{eqnarray*}](../../_images/math/a390dc04d74d496c7361dc92dae947bf9418b104.png)
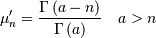

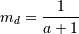
![h\left[X\right]=a-\left(a+1\right)\Psi\left(a\right)+\log\Gamma\left(a\right).](../../_images/math/ee1f7456fb174b88d83fb4e3574253ce669b84fc.png)
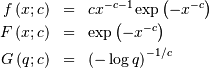
![h\left[X\right]=1+\gamma+\frac{\gamma}{c}-\log\left(c\right)](../../_images/math/48a07a4ce4cd42b82c8f2ce3c68388eb0a9da011.png)
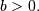
![\begin{eqnarray*} f\left(x;a,b\right) & = & \frac{b}{x\left(1-x\right)}\phi\left(a+b\log\frac{x}{1-x}\right)\\ F\left(x;a,b\right) & = & \Phi\left(a+b\log\frac{x}{1-x}\right)\\ G\left(q;a,b\right) & = & \frac{1}{1+\exp\left[-\frac{1}{b}\left(\Phi^{-1}\left(q\right)-a\right)\right]}\end{eqnarray*}](../../_images/math/0dd10bea4e56b7e920bf970175412edf682a23ea.png)
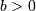 .
.![\begin{eqnarray*} f\left(x;a,b\right) & = & \frac{b}{\sqrt{x^{2}+1}}\phi\left(a+b\log\left(x+\sqrt{x^{2}+1}\right)\right)\\ F\left(x;a,b\right) & = & \Phi\left(a+b\log\left(x+\sqrt{x^{2}+1}\right)\right)\\ G\left(q;a,b\right) & = & \sinh\left[\frac{\Phi^{-1}\left(q\right)-a}{b}\right]\end{eqnarray*}](../../_images/math/ea9f8fe2e01fa5c60a518a883741d1ab7cc32193.png)
![\begin{eqnarray*} f\left(x\right) & = & \frac{\exp\left(-x\right)}{\left[1+\exp\left(-x\right)\right]^{2}}\\ F\left(x\right) & = & \frac{1}{1+\exp\left(-x\right)}\\ G\left(q\right) & = & -\log\left(1/q-1\right)\end{eqnarray*}](../../_images/math/6ed3a0c77154085a9d5845f91aca2663df2f8ac3.png)
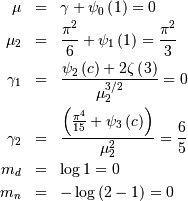
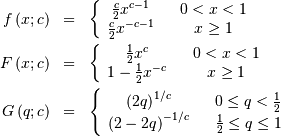
![h\left[X\right]=\log\left(\frac{2e}{c}\right)](../../_images/math/8f11cc455a43203e25431ec0da7ceb8528889c58.png)
![\begin{eqnarray*} f\left(x;c\right) & = & \frac{\exp\left(cx-e^{x}\right)}{\Gamma\left(c\right)}\\ F\left(x;c\right) & = & \frac{\Gamma\left(c,e^{x}\right)}{\Gamma\left(c\right)}\\ G\left(q;c\right) & = & \log\left[\Gamma^{-1}\left[c,q\Gamma\left(c\right)\right]\right]\end{eqnarray*}](../../_images/math/ed779b24ac02cc2c8f629ca2f49eb4f37c656cdf.png)
![\mu_{n}^{\prime}=\int_{0}^{\infty}\left[\log y\right]^{n}y^{c-1}\exp\left(-y\right)dy.](../../_images/math/1c83538f61da9bc279ff11b552ebc694a7513ccf.png)
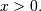
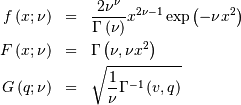
![\begin{eqnarray*} \mu & = & \frac{\Gamma\left(\nu+\frac{1}{2}\right)}{\sqrt{\nu}\Gamma\left(\nu\right)}\\ \mu_{2} & = & \left[1-\mu^{2}\right]\\ \gamma_{1} & = & \frac{\mu\left(1-4v\mu_{2}\right)}{2\nu\mu_{2}^{3/2}}\\ \gamma_{2} & = & \frac{-6\mu^{4}\nu+\left(8\nu-2\right)\mu^{2}-2\nu+1}{\nu\mu_{2}^{2}}\end{eqnarray*}](../../_images/math/08c4c835ca0587050996a2b6f88b480622983bf6.png)
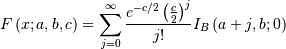
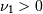 and
and 
![\begin{eqnarray*} f\left(x;\lambda,\nu_{1},\nu_{2}\right) & = & \exp\left[\frac{\lambda}{2}+\frac{\left(\lambda\nu_{1}x\right)}{2\left(\nu_{1}x+\nu_{2}\right)}\right]\nu_{1}^{\nu_{1}/2}\nu_{2}^{\nu_{2}/2}x^{\nu_{1}/2-1}\\ & & \times\left(\nu_{2}+\nu_{1}x\right)^{-\left(\nu_{1}+\nu_{2}\right)/2}\frac{\Gamma\left(\frac{\nu_{1}}{2}\right)\Gamma\left(1+\frac{\nu_{2}}{2}\right)L_{\nu_{2}/2}^{\nu_{1}/2-1}\left(-\frac{\lambda\nu_{1}x}{2\left(\nu_{1}x+\nu_{2}\right)}\right)}{B\left(\frac{\nu_{1}}{2},\frac{\nu_{2}}{2}\right)\Gamma\left(\frac{\nu_{1}+\nu_{2}}{2}\right)}\end{eqnarray*}](../../_images/math/196e53ae3ec2f834273c1aa55050126eaf93b8e0.png)
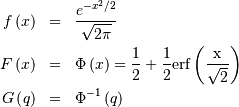
 and
and 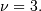
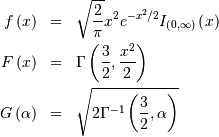
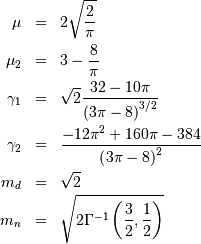
![h\left[X\right]=\log\left(\sqrt{\frac{2\pi}{e}}\right)+\gamma.](../../_images/math/05cef5440998c19fa6f28e60eb0440895630bf5c.png)
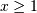 and
and 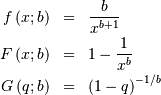
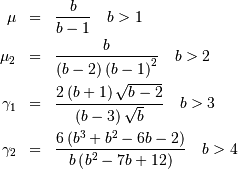
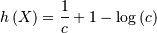
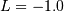 so
so 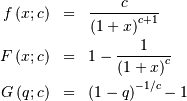
![h\left[X\right]=\frac{1}{c}+1-\log\left(c\right).](../../_images/math/bebb96156bf3868464a0a3a907f3e6118f759835.png)
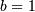 : defined for
: defined for 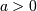
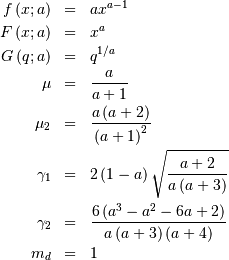
![h\left[X\right]=1-\frac{1}{a}-\log\left(a\right)](../../_images/math/fba000e7a64ddc3dad422c5c77d87d763801d679.png)
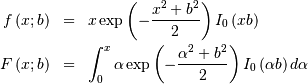
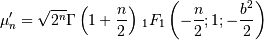
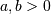
![x\in\left[a,b\right]](../../_images/math/d78a19d41baebb64b7c7300bc11f01e12db22ab7.png)

![\begin{eqnarray*} d & = & \log\left(a/b\right)\\ \mu & = & \frac{a-b}{d}\\ \mu_{2} & = & \mu\frac{a+b}{2}-\mu^{2}=\frac{\left(a-b\right)\left[a\left(d-2\right)+b\left(d+2\right)\right]}{2d^{2}}\\ \gamma_{1} & = & \frac{\sqrt{2}\left[12d\left(a-b\right)^{2}+d^{2}\left(a^{2}\left(2d-9\right)+2abd+b^{2}\left(2d+9\right)\right)\right]}{3d\sqrt{a-b}\left[a\left(d-2\right)+b\left(d+2\right)\right]^{3/2}}\\ \gamma_{2} & = & \frac{-36\left(a-b\right)^{3}+36d\left(a-b\right)^{2}\left(a+b\right)-16d^{2}\left(a^{3}-b^{3}\right)+3d^{3}\left(a^{2}+b^{2}\right)\left(a+b\right)}{3\left(a-b\right)\left[a\left(d-2\right)+b\left(d+2\right)\right]^{2}}-3\\ m_{d} & = & a\\ m_{n} & = & \sqrt{ab}\end{eqnarray*}](../../_images/math/11cf8269f10d83d44cd964349ad306e83b7bea1b.png)
![h\left[X\right]=\frac{1}{2}\log\left(ab\right)+\log\left[\log\left(\frac{b}{a}\right)\right].](../../_images/math/6e655ddd6598446507f83a0ac811f5125dc8799f.png)
 defined for
defined for 
![\begin{eqnarray*} f\left(x\right) & = & \frac{2}{\pi}\sqrt{1-x^{2}}\\ F\left(x\right) & = & \frac{1}{2}+\frac{1}{\pi}\left[x\sqrt{1-x^{2}}+\arcsin x\right]\\ G\left(q\right) & = & F^{-1}\left(q\right)\end{eqnarray*}](../../_images/math/04a2df9a80618668a6a7b121f57cdfc36e56cf03.png)
![h\left[X\right]=0.64472988584940017414.](../../_images/math/4e6020d362eb56ddab0673488979cef3666d20f5.png)
![\begin{eqnarray*} f\left(x;\lambda\right) & = & F^{\prime}\left(x;\lambda\right)=\frac{1}{G^{\prime}\left(F\left(x;\lambda\right);\lambda\right)}=\frac{1}{F^{\lambda-1}\left(x;\lambda\right)+\left[1-F\left(x;\lambda\right)\right]^{\lambda-1}}\\ F\left(x;\lambda\right) & = & G^{-1}\left(x;\lambda\right)\\ G\left(p;\lambda\right) & = & \frac{p^{\lambda}-\left(1-p\right)^{\lambda}}{\lambda}\end{eqnarray*}](../../_images/math/4003bdd8e3d9d99b4e70deb05d06ac732aa673a1.png)
![\begin{eqnarray*} h\left[X\right] & = & \int_{0}^{1}\log\left[G^{\prime}\left(p\right)\right]dp\\ & = & \int_{0}^{1}\log\left[p^{\lambda-1}+\left(1-p\right)^{\lambda-1}\right]dp.\end{eqnarray*}](../../_images/math/93aae2510a8a6d6d3b63fa228d7faa076fc12625.png)
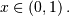 In general form, the lower limit is
In general form, the lower limit is 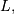 the upper limit is
the upper limit is 
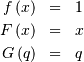
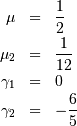
![h\left[X\right]=0](../../_images/math/f38cca81c2a51c2aa14296072447b9a77d94763c.png)
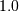 . Defined for
. Defined for 
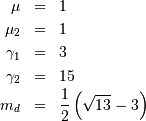
![x\in\left[0,2\pi\right]](../../_images/math/5d207ad45ccf2c56ea46002a8d846474099d1467.png)
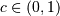
![\begin{eqnarray*} f\left(x;c\right) & = & \frac{1-c^{2}}{2\pi\left(1+c^{2}-2c\cos x\right)}\\ g_{c}\left(x\right) & = & \frac{1}{\pi}\arctan\left[\frac{1+c}{1-c}\tan\left(\frac{x}{2}\right)\right]\\ r_{c}\left(q\right) & = & 2\arctan\left[\frac{1-c}{1+c}\tan\left(\pi q\right)\right]\\ F\left(x;c\right) & = & \left\{ \begin{array}{ccc} g_{c}\left(x\right) & & 0\leq x<\pi\\ 1-g_{c}\left(2\pi-x\right) & & \pi\leq x\leq2\pi\end{array}\right.\\ G\left(q;c\right) & = & \left\{ \begin{array}{ccc} r_{c}\left(q\right) & & 0\leq q<\frac{1}{2}\\ 2\pi-r_{c}\left(1-q\right) & & \frac{1}{2}\leq q\leq1\end{array}\right.\end{eqnarray*}](../../_images/math/a9823f525a28fee5b60c1372fa0b32d8be556d26.png)
![h\left[X\right]=\log\left(2\pi\left(1-c^{2}\right)\right).](../../_images/math/a7df2b016fd9577f2e976a3dc13b0dfe7889cfb1.png)