scipy.stats.skellam

scipy.stats.skellam = <scipy.stats._discrete_distns.skellam_gen object at 0x7f4758307bd0>

A Skellam discrete random variable.

Discrete random variables are defined from a standard form and may require some shape parameters to complete its specification. Any optional keyword parameters can be passed to the methods of the RV object as given below:

Parameters:

x : array_like

quantiles

q : array_like

lower or upper tail probability

mu1, mu2 : array_like

shape parameters

loc : array_like, optional

location parameter (default=0)

size : int or tuple of ints, optional

shape of random variates (default computed from input arguments )

moments : str, optional

composed of letters [‘mvsk’] specifying which moments to compute where ‘m’ = mean, ‘v’ = variance, ‘s’ = (Fisher’s) skew and ‘k’ = (Fisher’s) kurtosis. (default=’mv’)

Alternatively, the object may be called (as a function) to fix the shape and

location parameters returning a “frozen” discrete RV object:

rv = skellam(mu1, mu2, loc=0)

• Frozen RV object with the same methods but holding the given shape and location fixed.

Notes

Probability distribution of the difference of two correlated or uncorrelated Poisson random variables.

Let k1 and k2 be two Poisson-distributed r.v. with expected values lam1 and lam2. Then, k1 - k2 follows a Skellam distribution with parameters mu1 = lam1 - rho*sqrt(lam1*lam2) and mu2 = lam2 - rho*sqrt(lam1*lam2), where rho is the correlation coefficient between k1 and k2. If the two Poisson-distributed r.v. are independent then rho = 0.

Parameters mu1 and mu2 must be strictly positive.

For details see: http://en.wikipedia.org/wiki/Skellam_distribution

skellam takes mu1 and mu2 as shape parameters.

Examples

>>> from scipy.stats import skellam
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

Calculate a few first moments:

>>> mu1, mu2 = 15, 8
>>> mean, var, skew, kurt = skellam.stats(mu1, mu2, moments='mvsk')

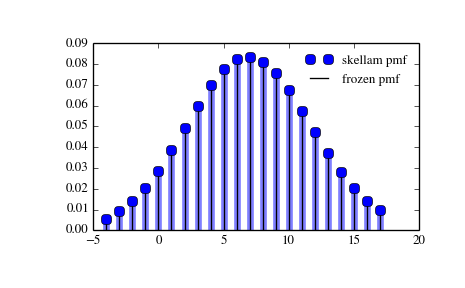
Display the probability mass function (pmf):

>>> x = np.arange(skellam.ppf(0.01, mu1, mu2),
...               skellam.ppf(0.99, mu1, mu2))
>>> ax.plot(x, skellam.pmf(x, mu1, mu2), 'bo', ms=8, label='skellam pmf')
>>> ax.vlines(x, 0, skellam.pmf(x, mu1, mu2), colors='b', lw=5, alpha=0.5)

Alternatively, freeze the distribution and display the frozen pmf:

>>> rv = skellam(mu1, mu2)
>>> ax.vlines(x, 0, rv.pmf(x), colors='k', linestyles='-', lw=1,
...         label='frozen pmf')
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

(Source code)

Check accuracy of cdf and ppf:

>>> prob = skellam.cdf(x, mu1, mu2)
>>> np.allclose(x, skellam.ppf(prob, mu1, mu2))
True

Generate random numbers:

>>> r = skellam.rvs(mu1, mu2, size=1000)

Methods

rvs(mu1, mu2, loc=0, size=1)	Random variates.
pmf(x, mu1, mu2, loc=0)	Probability mass function.
logpmf(x, mu1, mu2, loc=0)	Log of the probability mass function.
cdf(x, mu1, mu2, loc=0)	Cumulative density function.
logcdf(x, mu1, mu2, loc=0)	Log of the cumulative density function.
sf(x, mu1, mu2, loc=0)	Survival function (1-cdf — sometimes more accurate).
logsf(x, mu1, mu2, loc=0)	Log of the survival function.
ppf(q, mu1, mu2, loc=0)	Percent point function (inverse of cdf — percentiles).
isf(q, mu1, mu2, loc=0)	Inverse survival function (inverse of sf).
stats(mu1, mu2, loc=0, moments=’mv’)	Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(mu1, mu2, loc=0)	(Differential) entropy of the RV.
expect(func, mu1, mu2, loc=0, lb=None, ub=None, conditional=False)	Expected value of a function (of one argument) with respect to the distribution.
median(mu1, mu2, loc=0)	Median of the distribution.
mean(mu1, mu2, loc=0)	Mean of the distribution.
var(mu1, mu2, loc=0)	Variance of the distribution.
std(mu1, mu2, loc=0)	Standard deviation of the distribution.
interval(alpha, mu1, mu2, loc=0)	Endpoints of the range that contains alpha percent of the distribution