Discrete Statistical Distributions¶
Discrete random variables take on only a countable number of values.
The commonly used distributions are included in SciPy and described in
this document. Each discrete distribution can take one extra integer
parameter: 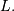 The relationship between the general distribution
The relationship between the general distribution
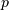 and the standard distribution
and the standard distribution 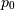 is
is
![\[ p\left(x\right)=p_{0}\left(x-L\right)\]](../../_images/math/da2c2afc808bfc737a3dc73cb9374658f9893722.png)
which allows for shifting of the input. When a distribution generator
is initialized, the discrete distribution can either specify the
beginning and ending (integer) values  and
and  which must be such that
which must be such that
![\[ p_{0}\left(x\right)=0\quad x<a\textrm{ or }x>b\]](../../_images/math/f9c1221310909ee5022d188882288c5ba4175749.png)
in which case, it is assumed that the pdf function is specified on the
integers 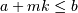 where
where 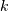 is a non-negative integer (
is a non-negative integer ( 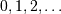 ) and
) and  is a positive integer multiplier. Alternatively, the two lists
is a positive integer multiplier. Alternatively, the two lists 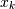 and
and 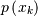 can be provided directly in which case a dictionary is set up
internally to evaulate probabilities and generate random variates.
can be provided directly in which case a dictionary is set up
internally to evaulate probabilities and generate random variates.
Probability Mass Function (PMF)¶
The probability mass function of a random variable X is defined as the probability that the random variable takes on a particular value.
![\[ p\left(x_{k}\right)=P\left[X=x_{k}\right]\]](../../_images/math/e257ac3c21d73e4af524649a3bd1d203b520f52b.png)
This is also sometimes called the probability density function, although technically
![\[ f\left(x\right)=\sum_{k}p\left(x_{k}\right)\delta\left(x-x_{k}\right)\]](../../_images/math/1bc46679ba63a3970d2ccb78f5cf2833fe35fa38.png)
is the probability density function for a discrete distribution [1] .
| [1] | XXX: Unknown layout Plain Layout: Note that we will be using 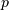 to represent the probability mass function and a parameter (a
XXX: probability). The usage should be obvious from context. to represent the probability mass function and a parameter (a
XXX: probability). The usage should be obvious from context. |
Cumulative Distribution Function (CDF)¶
The cumulative distribution function is
![\[ F\left(x\right)=P\left[X\leq x\right]=\sum_{x_{k}\leq x}p\left(x_{k}\right)\]](../../_images/math/7538fb54cd813b3b89db6fa2c79dd157b610c49f.png)
and is also useful to be able to compute. Note that
![\[ F\left(x_{k}\right)-F\left(x_{k-1}\right)=p\left(x_{k}\right)\]](../../_images/math/b7000a7abe4af9b9158280d047f4daf19ddc97df.png)
Survival Function¶
The survival function is just
![\[ S\left(x\right)=1-F\left(x\right)=P\left[X>k\right]\]](../../_images/math/46b2a4a8aebbd9885a6795e4d15f95305c8f9f7e.png)
the probability that the random variable is strictly larger than 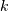 .
.
Percent Point Function (Inverse CDF)¶
The percent point function is the inverse of the cumulative distribution function and is
![\[ G\left(q\right)=F^{-1}\left(q\right)\]](../../_images/math/ab187cccee202d3c41dcfc27237c41b8764ac6f9.png)
for discrete distributions, this must be modified for cases where
there is no 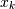 such that
such that 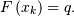 In these cases we choose
In these cases we choose 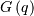 to be the smallest value
to be the smallest value 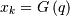 for which
for which 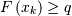 . If
. If 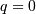 then we define
then we define 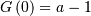 . This definition allows random variates to be defined in the same way
as with continuous rv’s using the inverse cdf on a uniform
distribution to generate random variates.
. This definition allows random variates to be defined in the same way
as with continuous rv’s using the inverse cdf on a uniform
distribution to generate random variates.
Inverse survival function¶
The inverse survival function is the inverse of the survival function
![\[ Z\left(\alpha\right)=S^{-1}\left(\alpha\right)=G\left(1-\alpha\right)\]](../../_images/math/71aa00d920522c0f57aeba5b958e4ae96c4fc862.png)
and is thus the smallest non-negative integer 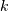 for which
for which 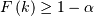 or the smallest non-negative integer
or the smallest non-negative integer 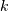 for which
for which 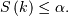
Hazard functions¶
If desired, the hazard function and the cumulative hazard function could be defined as
![\[ h\left(x_{k}\right)=\frac{p\left(x_{k}\right)}{1-F\left(x_{k}\right)}\]](../../_images/math/f20bde06a918b4b82743c310caa60bb7d6eee0cd.png)
and
![\[ H\left(x\right)=\sum_{x_{k}\leq x}h\left(x_{k}\right)=\sum_{x_{k}\leq x}\frac{F\left(x_{k}\right)-F\left(x_{k-1}\right)}{1-F\left(x_{k}\right)}.\]](../../_images/math/594bef2ea8a44334ea361be3a1f24167d6499ab7.png)
Moments¶
Non-central moments are defined using the PDF
![\[ \mu_{m}^{\prime}=E\left[X^{m}\right]=\sum_{k}x_{k}^{m}p\left(x_{k}\right).\]](../../_images/math/8ab12e600a5b8ea792bf026d11c682fe99242828.png)
Central moments are computed similarly 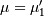
![\begin{eqnarray*} \mu_{m}=E\left[\left(X-\mu\right)^{m}\right] & = & \sum_{k}\left(x_{k}-\mu\right)^{m}p\left(x_{k}\right)\\ & = & \sum_{k=0}^{m}\left(-1\right)^{m-k}\left(\begin{array}{c} m\\ k\end{array}\right)\mu^{m-k}\mu_{k}^{\prime}\end{eqnarray*}](../../_images/math/2d0dfc52a5db6340e07751ef5e63fbff12a4dc19.png)
The mean is the first moment
![\[ \mu=\mu_{1}^{\prime}=E\left[X\right]=\sum_{k}x_{k}p\left(x_{k}\right)\]](../../_images/math/750ec320fe8416b688400d53a7222bc380f2fa64.png)
the variance is the second central moment
![\[ \mu_{2}=E\left[\left(X-\mu\right)^{2}\right]=\sum_{x_{k}}x_{k}^{2}p\left(x_{k}\right)-\mu^{2}.\]](../../_images/math/5d51609c27ec6ec3905ef637ca2bdae39f52efc5.png)
Skewness is defined as
![\[ \gamma_{1}=\frac{\mu_{3}}{\mu_{2}^{3/2}}\]](../../_images/math/303f296585f63e52a50c3dc29fc3fca5217b299e.png)
while (Fisher) kurtosis is
![\[ \gamma_{2}=\frac{\mu_{4}}{\mu_{2}^{2}}-3,\]](../../_images/math/2e9d66b9f7eda6d6377d99df415c96678cc4c338.png)
so that a normal distribution has a kurtosis of zero.
Moment generating function¶
The moment generating function is defined as
![\[ M_{X}\left(t\right)=E\left[e^{Xt}\right]=\sum_{x_{k}}e^{x_{k}t}p\left(x_{k}\right)\]](../../_images/math/d2f9f1d22e1ee5b8d8353b1117f65ba8667c93b1.png)
Moments are found as the derivatives of the moment generating function
evaluated at 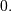
Fitting data¶
To fit data to a distribution, maximizing the likelihood function is common. Alternatively, some distributions have well-known minimum variance unbiased estimators. These will be chosen by default, but the likelihood function will always be available for minimizing.
If 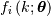 is the PDF of a random-variable where
is the PDF of a random-variable where 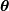 is a vector of parameters ( e.g.
is a vector of parameters ( e.g. 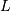 and
and 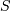 ), then for a collection of
), then for a collection of 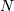 independent samples from this distribution, the joint distribution the
random vector
independent samples from this distribution, the joint distribution the
random vector 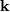 is
is
![\[ f\left(\mathbf{k};\boldsymbol{\theta}\right)=\prod_{i=1}^{N}f_{i}\left(k_{i};\boldsymbol{\theta}\right).\]](../../_images/math/7f057e1b247468c082d4a7e370cfebc97c903a1e.png)
The maximum likelihood estimate of the parameters 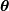 are the parameters which maximize this function with
are the parameters which maximize this function with 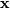 fixed and given by the data:
fixed and given by the data:
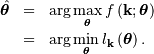
Where
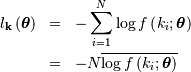
Combinations¶
Note that
![\[ k!=k\cdot\left(k-1\right)\cdot\left(k-2\right)\cdot\cdots\cdot1=\Gamma\left(k+1\right)\]](../../_images/math/69038bdea2b8d1487890c43f4be3e939a59df0be.png)
and has special cases of
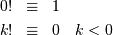
and
![\[ \left(\begin{array}{c} n\\ k\end{array}\right)=\frac{n!}{\left(n-k\right)!k!}.\]](../../_images/math/f6649ca900cd632c93cb5686364fc1f7a4fb5b9c.png)
If 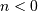 or
or 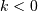 or
or 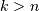 we define
we define 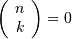
Bernoulli¶
A Bernoulli random variable of parameter 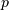 takes one of only two values
takes one of only two values 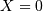 or
or 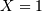 . The probability of success (
. The probability of success ( 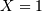 ) is
) is 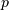 , and the probability of failure (
, and the probability of failure ( 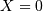 ) is
) is 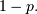 It can be thought of as a binomial random variable with
It can be thought of as a binomial random variable with 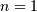 . The PMF is
. The PMF is 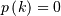 for
for 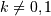 and
and
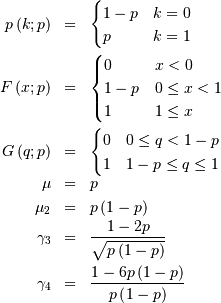
![\[ M\left(t\right)=1-p\left(1-e^{t}\right)\]](../../_images/math/574972c45725200ba0c2096be00bb8a355abd06a.png)
![\[ \mu_{m}^{\prime}=p\]](../../_images/math/0084df2d9f3f1ba8dda542a7f99a5d044c441249.png)
![\[ h\left[X\right]=p\log p+\left(1-p\right)\log\left(1-p\right)\]](../../_images/math/51975e6544e54d117d37015e46e14833b7980f46.png)
Binomial¶
A binomial random variable with parameters 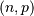 can be described as the sum of
can be described as the sum of  independent Bernoulli random variables of parameter
independent Bernoulli random variables of parameter 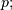
![\[ Y=\sum_{i=1}^{n}X_{i}.\]](../../_images/math/95158d7d06142de93efbbc36f4ab9521718cdee7.png)
Therefore, this random variable counts the number of successes in  independent trials of a random experiment where the probability of
success is
independent trials of a random experiment where the probability of
success is 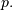
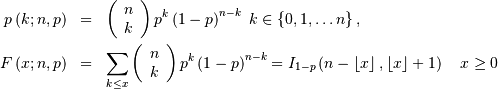
where the incomplete beta integral is
![\[ I_{x}\left(a,b\right)=\frac{\Gamma\left(a+b\right)}{\Gamma\left(a\right)\Gamma\left(b\right)}\int_{0}^{x}t^{a-1}\left(1-t\right)^{b-1}dt.\]](../../_images/math/8b35192c943bd7ae32db2087c63795fab17c3f5c.png)
Now
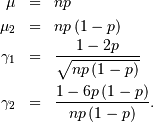
![\[ M\left(t\right)=\left[1-p\left(1-e^{t}\right)\right]^{n}\]](../../_images/math/ced5e926304fb3bed802b51a065d14922b2e1f0d.png)
Planck (discrete exponential)¶
Named Planck because of its relationship to the black-body problem he solved.
![\begin{eqnarray*} p\left(k;\lambda\right) & = & \left(1-e^{-\lambda}\right)e^{-\lambda k}\quad k\lambda\geq0\\ F\left(x;\lambda\right) & = & 1-e^{-\lambda\left(\left\lfloor x\right\rfloor +1\right)}\quad x\lambda\geq0\\ G\left(q;\lambda\right) & = & \left\lceil -\frac{1}{\lambda}\log\left[1-q\right]-1\right\rceil .\end{eqnarray*}](../../_images/math/9d943e9cd09cb73d948ac2d071a7a14768533627.png)
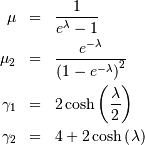
![\[ M\left(t\right)=\frac{1-e^{-\lambda}}{1-e^{t-\lambda}}\]](../../_images/math/ae91193aa3a39728fccc997b673c1f63382454f9.png)
![\[ h\left[X\right]=\frac{\lambda e^{-\lambda}}{1-e^{-\lambda}}-\log\left(1-e^{-\lambda}\right)\]](../../_images/math/8844292823e76999ef4b36f99e1031af5568bd94.png)
Poisson¶
The Poisson random variable counts the number of successes in  independent Bernoulli trials in the limit as
independent Bernoulli trials in the limit as 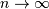 and
and 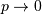 where the probability of success in each trial is
where the probability of success in each trial is 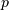 and
and 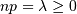 is a constant. It can be used to approximate the Binomial random
variable or in it’s own right to count the number of events that occur
in the interval
is a constant. It can be used to approximate the Binomial random
variable or in it’s own right to count the number of events that occur
in the interval ![\left[0,t\right]](../../_images/math/4de574753214917bd8d2daba3364f8c0030b495e.png) for a process satisfying certain “sparsity “constraints. The functions are
for a process satisfying certain “sparsity “constraints. The functions are
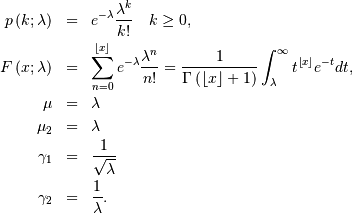
![\[ M\left(t\right)=\exp\left[\lambda\left(e^{t}-1\right)\right].\]](../../_images/math/e78c9998900922361d5f0a729da695667232a832.png)
Geometric¶
The geometric random variable with parameter 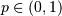 can be defined as the number of trials required to obtain a success
where the probability of success on each trial is
can be defined as the number of trials required to obtain a success
where the probability of success on each trial is 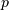 . Thus,
. Thus,
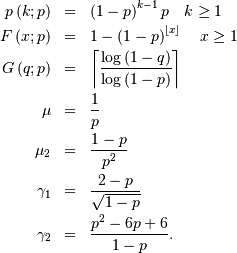
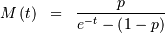
Negative Binomial¶
The negative binomial random variable with parameters  and
and 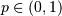 can be defined as the number of extra independent trials (beyond
can be defined as the number of extra independent trials (beyond  ) required to accumulate a total of
) required to accumulate a total of  successes where the probability of a success on each trial is
successes where the probability of a success on each trial is 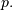 Equivalently, this random variable is the number of failures
encoutered while accumulating
Equivalently, this random variable is the number of failures
encoutered while accumulating  successes during independent trials of an experiment that succeeds
with probability
successes during independent trials of an experiment that succeeds
with probability 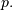 Thus,
Thus,
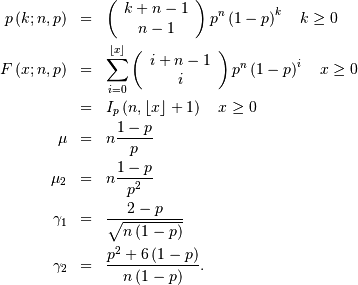
Recall that 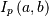 is the incomplete beta integral.
is the incomplete beta integral.
Hypergeometric¶
The hypergeometric random variable with parameters 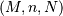 counts the number of “good “objects in a sample of size
counts the number of “good “objects in a sample of size 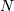 chosen without replacement from a population of
chosen without replacement from a population of 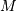 objects where
objects where  is the number of “good “objects in the total population.
is the number of “good “objects in the total population.
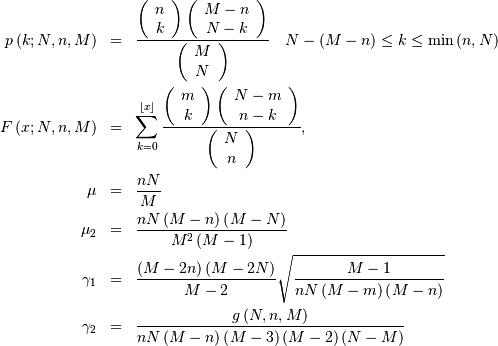
where (defining 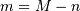 )
)
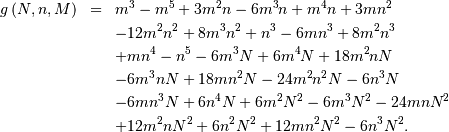
Zipf (Zeta)¶
A random variable has the zeta distribution (also called the zipf
distribution) with parameter 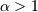 if it’s probability mass function is given by
if it’s probability mass function is given by
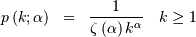
where
![\[ \zeta\left(\alpha\right)=\sum_{n=1}^{\infty}\frac{1}{n^{\alpha}}\]](../../_images/math/34138f21edadb88957283c28a3879c0ca674e564.png)
is the Riemann zeta function. Other functions of this distribution are
![\begin{eqnarray*} F\left(x;\alpha\right) & = & \frac{1}{\zeta\left(\alpha\right)}\sum_{k=1}^{\left\lfloor x\right\rfloor }\frac{1}{k^{\alpha}}\\ \mu & = & \frac{\zeta_{1}}{\zeta_{0}}\quad\alpha>2\\ \mu_{2} & = & \frac{\zeta_{2}\zeta_{0}-\zeta_{1}^{2}}{\zeta_{0}^{2}}\quad\alpha>3\\ \gamma_{1} & = & \frac{\zeta_{3}\zeta_{0}^{2}-3\zeta_{0}\zeta_{1}\zeta_{2}+2\zeta_{1}^{3}}{\left[\zeta_{2}\zeta_{0}-\zeta_{1}^{2}\right]^{3/2}}\quad\alpha>4\\ \gamma_{2} & = & \frac{\zeta_{4}\zeta_{0}^{3}-4\zeta_{3}\zeta_{1}\zeta_{0}^{2}+12\zeta_{2}\zeta_{1}^{2}\zeta_{0}-6\zeta_{1}^{4}-3\zeta_{2}^{2}\zeta_{0}^{2}}{\left(\zeta_{2}\zeta_{0}-\zeta_{1}^{2}\right)^{2}}.\end{eqnarray*}](../../_images/math/74d879839e4156e47298b6e8b049e1dcee18afb0.png)
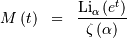
where 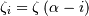 and
and 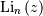 is the
is the 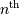 polylogarithm function of
polylogarithm function of  defined as
defined as
![\[ \textrm{Li}_{n}\left(z\right)\equiv\sum_{k=1}^{\infty}\frac{z^{k}}{k^{n}}\]](../../_images/math/01d5a3d00e968d2efee516ed8961fa7cf787cfe1.png)
![\[ \mu_{n}^{\prime}=\left.M^{\left(n\right)}\left(t\right)\right|_{t=0}=\left.\frac{\textrm{Li}_{\alpha-n}\left(e^{t}\right)}{\zeta\left(a\right)}\right|_{t=0}=\frac{\zeta\left(\alpha-n\right)}{\zeta\left(\alpha\right)}\]](../../_images/math/9e49184faef5fd0e283fe8dd214330e80002d1d4.png)
Logarithmic (Log-Series, Series)¶
The logarimthic distribution with parameter 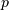 has a probability mass function with terms proportional to the Taylor
series expansion of
has a probability mass function with terms proportional to the Taylor
series expansion of 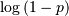
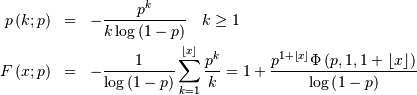
where
![\[ \Phi\left(z,s,a\right)=\sum_{k=0}^{\infty}\frac{z^{k}}{\left(a+k\right)^{s}}\]](../../_images/math/f42dabe7912c7ab5e492c645af972e7f013e4baa.png)
is the Lerch Transcendent. Also define 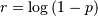
![\begin{eqnarray*} \mu & = & -\frac{p}{\left(1-p\right)r}\\ \mu_{2} & = & -\frac{p\left[p+r\right]}{\left(1-p\right)^{2}r^{2}}\\ \gamma_{1} & = & -\frac{2p^{2}+3pr+\left(1+p\right)r^{2}}{r\left(p+r\right)\sqrt{-p\left(p+r\right)}}r\\ \gamma_{2} & = & -\frac{6p^{3}+12p^{2}r+p\left(4p+7\right)r^{2}+\left(p^{2}+4p+1\right)r^{3}}{p\left(p+r\right)^{2}}.\end{eqnarray*}](../../_images/math/2b78ebedd1af6dd6c30cc68676121dc6173a26fe.png)
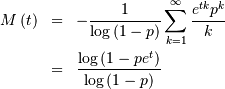
Thus,
![\[ \mu_{n}^{\prime}=\left.M^{\left(n\right)}\left(t\right)\right|_{t=0}=\left.\frac{\textrm{Li}_{1-n}\left(pe^{t}\right)}{\log\left(1-p\right)}\right|_{t=0}=-\frac{\textrm{Li}_{1-n}\left(p\right)}{\log\left(1-p\right)}.\]](../../_images/math/6f143327981ca88bed9be0ff8c7eb1dcd691512b.png)
Discrete Uniform (randint)¶
The discrete uniform distribution with parameters 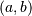 constructs a random variable that has an equal probability of being
any one of the integers in the half-open range
constructs a random variable that has an equal probability of being
any one of the integers in the half-open range 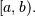 If
If  is not given it is assumed to be zero and the only parameter is
is not given it is assumed to be zero and the only parameter is 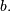 Therefore,
Therefore,
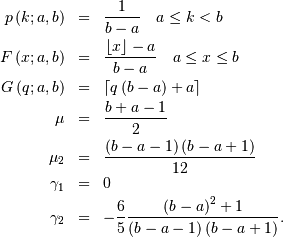
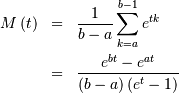
Discrete Laplacian¶
Defined over all integers for 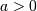
![\begin{eqnarray*} p\left(k\right) & = & \tanh\left(\frac{a}{2}\right)e^{-a\left|k\right|},\\ F\left(x\right) & = & \left\{ \begin{array}{cc} \frac{e^{a\left(\left\lfloor x\right\rfloor +1\right)}}{e^{a}+1} & \left\lfloor x\right\rfloor <0,\\ 1-\frac{e^{-a\left\lfloor x\right\rfloor }}{e^{a}+1} & \left\lfloor x\right\rfloor \geq0.\end{array}\right.\\ G\left(q\right) & = & \left\{ \begin{array}{cc} \left\lceil \frac{1}{a}\log\left[q\left(e^{a}+1\right)\right]-1\right\rceil & q<\frac{1}{1+e^{-a}},\\ \left\lceil -\frac{1}{a}\log\left[\left(1-q\right)\left(1+e^{a}\right)\right]\right\rceil & q\geq\frac{1}{1+e^{-a}}.\end{array}\right.\end{eqnarray*}](../../_images/math/78dd4b6ff517ee7cc147ea9d1ae8482b17ee1106.png)
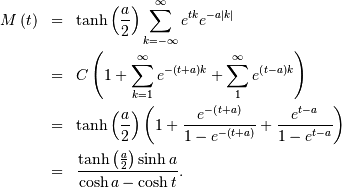
Thus,
![\[ \mu_{n}^{\prime}=M^{\left(n\right)}\left(0\right)=\left[1+\left(-1\right)^{n}\right]\textrm{Li}_{-n}\left(e^{-a}\right)\]](../../_images/math/11d59fe98a7943c36cbc3380a4f6971c16292f7f.png)
where 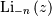 is the polylogarithm function of order
is the polylogarithm function of order 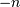 evaluated at
evaluated at 
![\[ h\left[X\right]=-\log\left(\tanh\left(\frac{a}{2}\right)\right)+\frac{a}{\sinh a}\]](../../_images/math/4c10a51accacf670d69653f9c33bc3c8dfd1decf.png)

![\[ \overline{y\left(\mathbf{x}\right)}=\frac{1}{N}\sum_{i=1}^{N}y\left(x_{i}\right)\]](../../_images/math/3b549f7423c0e53299a891d7eb6c311d91aef350.png)
![\begin{eqnarray*} p\left(k;N,\lambda\right) & = & \frac{1-e^{-\lambda}}{1-e^{-\lambda N}}\exp\left(-\lambda k\right)\quad k\in\left\{ 0,1,\ldots,N-1\right\} \\ F\left(x;N,\lambda\right) & = & \left\{ \begin{array}{cc} 0 & x<0\\ \frac{1-\exp\left[-\lambda\left(\left\lfloor x\right\rfloor +1\right)\right]}{1-\exp\left(-\lambda N\right)} & 0\leq x\leq N-1\\ 1 & x\geq N-1\end{array}\right.\\ G\left(q,\lambda\right) & = & \left\lceil -\frac{1}{\lambda}\log\left[1-q\left(1-e^{-\lambda N}\right)\right]-1\right\rceil \end{eqnarray*}](../../_images/math/9ab945d737ece1bc4e3553bfe47fb2e1e77f114f.png)
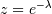
![\begin{eqnarray*} \mu & = & \frac{z}{1-z}-\frac{Nz^{N}}{1-z^{N}}\\ \mu_{2} & = & \frac{z}{\left(1-z\right)^{2}}-\frac{N^{2}z^{N}}{\left(1-z^{N}\right)^{2}}\\ \gamma_{1} & = & \frac{z\left(1+z\right)\left(\frac{1-z^{N}}{1-z}\right)^{3}-N^{3}z^{N}\left(1+z^{N}\right)}{\left[z\left(\frac{1-z^{N}}{1-z}\right)^{2}-N^{2}z^{N}\right]^{3/2}}\\ \gamma_{2} & = & \frac{z\left(1+4z+z^{2}\right)\left(\frac{1-z^{N}}{1-z}\right)^{4}-N^{4}z^{N}\left(1+4z^{N}+z^{2N}\right)}{\left[z\left(\frac{1-z^{N}}{1-z}\right)^{2}-N^{2}z^{N}\right]^{2}}\end{eqnarray*}](../../_images/math/42a820739fd98debf8689edfd38e88f2cf1a5e56.png)
![\[ M\left(t\right)=\frac{1-e^{N\left(t-\lambda\right)}}{1-e^{t-\lambda}}\frac{1-e^{-\lambda}}{1-e^{-\lambda N}}\]](../../_images/math/47455eb3b6056f05245cef63ba84658b2725faf3.png)
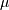 and
and  and
and ![\[ p\left(k;\mu,\lambda\right)=\frac{1}{Z\left(\lambda\right)}\exp\left[-\lambda\left(k-\mu\right)^{2}\right]\]](../../_images/math/e0c04f2e33f8f8346a0c16d9e3372b72046f70a2.png)
![\[ Z\left(\lambda\right)=\sum_{k=-\infty}^{\infty}\exp\left[-\lambda k^{2}\right]\]](../../_images/math/f82632477e2b917ff4fe7c376066db4d37e2cfd2.png)
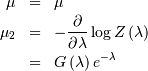
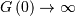 and
and 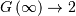 with a minimum less than 2 near
with a minimum less than 2 near 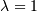
![\[ G\left(\lambda\right)=\frac{1}{Z\left(\lambda\right)}\sum_{k=-\infty}^{\infty}k^{2}\exp\left[-\lambda\left(k+1\right)\left(k-1\right)\right]\]](../../_images/math/1343ff0c6852e4adcb3d5913912ef9900ec48a1d.png)