scipy.signal.cheby1¶
- scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba')[source]¶
Chebyshev type I digital and analog filter design.
Design an Nth order digital or analog Chebyshev type I filter and return the filter coefficients in (B,A) or (Z,P,K) form.
Parameters: N : int
The order of the filter.
rp : float
The maximum ripple allowed below unity gain in the passband. Specified in decibels, as a positive number.
Wn : array_like
A scalar or length-2 sequence giving the critical frequencies. For Type I filters, this is the point in the transition band at which the gain first drops below -rp. For digital filters, Wn is normalized from 0 to 1, where 1 is the Nyquist frequency, pi radians/sample. (Wn is thus in half-cycles / sample.) For analog filters, Wn is an angular frequency (e.g. rad/s).
btype : {‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional
The type of filter. Default is ‘lowpass’.
analog : bool, optional
When True, return an analog filter, otherwise a digital filter is returned.
output : {‘ba’, ‘zpk’}, optional
Type of output: numerator/denominator (‘ba’) or pole-zero (‘zpk’). Default is ‘ba’.
Returns: b, a : ndarray, ndarray
Numerator (b) and denominator (a) polynomials of the IIR filter. Only returned if output='ba'.
z, p, k : ndarray, ndarray, float
Zeros, poles, and system gain of the IIR filter transfer function. Only returned if output='zpk'.
See also
Notes
The Chebyshev type I filter maximizes the rate of cutoff between the frequency response’s passband and stopband, at the expense of ripple in the passband and increased ringing in the step response.
Type I filters roll off faster than Type II (cheby2), but Type II filters do not have any ripple in the passband.
The equiripple passband has N maxima or minima (for example, a 5th-order filter has 3 maxima and 2 minima). Consequently, the DC gain is unity for odd-order filters, or -rp dB for even-order filters.
Examples
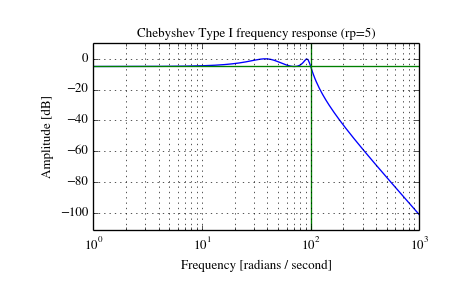
Plot the filter’s frequency response, showing the critical points:
>>> from scipy import signal >>> import matplotlib.pyplot as plt
>>> b, a = signal.cheby1(4, 5, 100, 'low', analog=True) >>> w, h = signal.freqs(b, a) >>> plt.plot(w, 20 * np.log10(abs(h))) >>> plt.xscale('log') >>> plt.title('Chebyshev Type I frequency response (rp=5)') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Amplitude [dB]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.axvline(100, color='green') # cutoff frequency >>> plt.axhline(-5, color='green') # rp >>> plt.show()