scipy.integrate.quad¶
- scipy.integrate.quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)[source]¶
Compute a definite integral.
Integrate func from a to b (possibly infinite interval) using a technique from the Fortran library QUADPACK.
Run scipy.integrate.quad_explain() for more information on the more esoteric inputs and outputs.
Parameters : func : function
A Python function or method to integrate. If func takes many arguments, it is integrated along the axis corresponding to the first argument.
a : float
Lower limit of integration (use -numpy.inf for -infinity).
b : float
Upper limit of integration (use numpy.inf for +infinity).
args : tuple, optional
Extra arguments to pass to func.
full_output : int, optional
Non-zero to return a dictionary of integration information. If non-zero, warning messages are also suppressed and the message is appended to the output tuple.
Returns : y : float
The integral of func from a to b.
abserr : float
An estimate of the absolute error in the result.
infodict : dict
A dictionary containing additional information. Run scipy.integrate.quad_explain() for more information.
message :
A convergence message.
explain :
Appended only with ‘cos’ or ‘sin’ weighting and infinite integration limits, it contains an explanation of the codes in infodict[‘ierlst’]
Other Parameters: epsabs : float or int, optional
Absolute error tolerance.
epsrel : float or int, optional
Relative error tolerance.
limit : float or int, optional
An upper bound on the number of subintervals used in the adaptive algorithm.
points : (sequence of floats,ints), optional
A sequence of break points in the bounded integration interval where local difficulties of the integrand may occur (e.g., singularities, discontinuities). The sequence does not have to be sorted.
weight : float or int, optional
String indicating weighting function.
wvar : optional
Variables for use with weighting functions.
wopts : optional
Optional input for reusing Chebyshev moments.
maxp1 : float or int, optional
An upper bound on the number of Chebyshev moments.
limlst : int, optional
Upper bound on the number of cylces (>=3) for use with a sinusoidal weighting and an infinite end-point.
See also
- dblquad
- double integral
- tplquad
- triple integral
- nquad
- n-dimensional integrals (uses quad recursively)
- fixed_quad
- fixed-order Gaussian quadrature
- quadrature
- adaptive Gaussian quadrature
- odeint
- ODE integrator
- ode
- ODE integrator
- simps
- integrator for sampled data
- romb
- integrator for sampled data
- scipy.special
- for coefficients and roots of orthogonal polynomials
Examples
Calculate
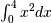 and compare with an analytic result
and compare with an analytic result>>> from scipy import integrate >>> x2 = lambda x: x**2 >>> integrate.quad(x2, 0, 4) (21.333333333333332, 2.3684757858670003e-13) >>> print(4**3 / 3.) # analytical result 21.3333333333
Calculate
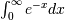
>>> invexp = lambda x: np.exp(-x) >>> integrate.quad(invexp, 0, np.inf) (1.0, 5.842605999138044e-11)
>>> f = lambda x,a : a*x >>> y, err = integrate.quad(f, 0, 1, args=(1,)) >>> y 0.5 >>> y, err = integrate.quad(f, 0, 1, args=(3,)) >>> y 1.5
