Signal Processing (scipy.signal)¶
The signal processing toolbox currently contains some filtering functions, a limited set of filter design tools, and a few B-spline interpolation algorithms for one- and two-dimensional data. While the B-spline algorithms could technically be placed under the interpolation category, they are included here because they only work with equally-spaced data and make heavy use of filter-theory and transfer-function formalism to provide a fast B-spline transform. To understand this section you will need to understand that a signal in SciPy is an array of real or complex numbers.
B-splines¶
A B-spline is an approximation of a continuous function over a finite-
domain in terms of B-spline coefficients and knot points. If the knot-
points are equally spaced with spacing 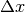 , then the B-spline
approximation to a 1-dimensional function is the finite-basis expansion.
, then the B-spline
approximation to a 1-dimensional function is the finite-basis expansion.
![\[ y\left(x\right)\approx\sum_{j}c_{j}\beta^{o}\left(\frac{x}{\Delta x}-j\right).\]](../_images/math/72f6427ffd1d252af16680e8de48a10dcd737e0a.png)
In two dimensions with knot-spacing 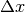 and
and 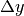 , the
function representation is
, the
function representation is
![\[ z\left(x,y\right)\approx\sum_{j}\sum_{k}c_{jk}\beta^{o}\left(\frac{x}{\Delta x}-j\right)\beta^{o}\left(\frac{y}{\Delta y}-k\right).\]](../_images/math/2f3334fe845a1261f3fb32eebc7fdfd7a691fa66.png)
In these expressions, 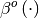 is the space-limited
B-spline basis function of order,
is the space-limited
B-spline basis function of order,  . The requirement of equally-spaced
knot-points and equally-spaced data points, allows the development of fast
(inverse-filtering) algorithms for determining the coefficients,
. The requirement of equally-spaced
knot-points and equally-spaced data points, allows the development of fast
(inverse-filtering) algorithms for determining the coefficients, 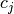 , from sample-values,
, from sample-values, 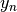 . Unlike the general spline interpolation
algorithms, these algorithms can quickly find the spline coefficients for large
images.
. Unlike the general spline interpolation
algorithms, these algorithms can quickly find the spline coefficients for large
images.
The advantage of representing a set of samples via B-spline basis functions is that continuous-domain operators (derivatives, re- sampling, integral, etc.) which assume that the data samples are drawn from an underlying continuous function can be computed with relative ease from the spline coefficients. For example, the second-derivative of a spline is
![\[ y{}^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\beta^{o\prime\prime}\left(\frac{x}{\Delta x}-j\right).\]](../_images/math/308f36cde9db42ef74e80f8a346d5943d4731583.png)
Using the property of B-splines that
![\[ \frac{d^{2}\beta^{o}\left(w\right)}{dw^{2}}=\beta^{o-2}\left(w+1\right)-2\beta^{o-2}\left(w\right)+\beta^{o-2}\left(w-1\right)\]](../_images/math/4a4eb9a63f1b21aa7018da70e32e029a369e3c31.png)
it can be seen that
![\[ y^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\left[\beta^{o-2}\left(\frac{x}{\Delta x}-j+1\right)-2\beta^{o-2}\left(\frac{x}{\Delta x}-j\right)+\beta^{o-2}\left(\frac{x}{\Delta x}-j-1\right)\right].\]](../_images/math/43a1ce2036c6d0d329fb3f91b97d673c0c1a30eb.png)
If 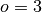 , then at the sample points,
, then at the sample points,
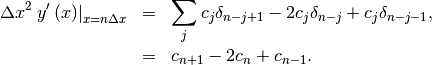
Thus, the second-derivative signal can be easily calculated from the spline fit. if desired, smoothing splines can be found to make the second-derivative less sensitive to random-errors.
The savvy reader will have already noticed that the data samples are related to the knot coefficients via a convolution operator, so that simple convolution with the sampled B-spline function recovers the original data from the spline coefficients. The output of convolutions can change depending on how boundaries are handled (this becomes increasingly more important as the number of dimensions in the data- set increases). The algorithms relating to B-splines in the signal- processing sub package assume mirror-symmetric boundary conditions. Thus, spline coefficients are computed based on that assumption, and data-samples can be recovered exactly from the spline coefficients by assuming them to be mirror-symmetric also.
Currently the package provides functions for determining second- and
third-order cubic spline coefficients from equally spaced samples in
one- and two-dimensions (signal.qspline1d,
signal.qspline2d, signal.cspline1d,
signal.cspline2d). The package also supplies a function (
signal.bspline ) for evaluating the bspline basis function,
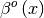 for arbitrary order and
for arbitrary order and 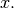 For
large
For
large  , the B-spline basis function can be approximated well
by a zero-mean Gaussian function with standard-deviation equal to
, the B-spline basis function can be approximated well
by a zero-mean Gaussian function with standard-deviation equal to
 :
:
![\[ \beta^{o}\left(x\right)\approx\frac{1}{\sqrt{2\pi\sigma_{o}^{2}}}\exp\left(-\frac{x^{2}}{2\sigma_{o}}\right).\]](../_images/math/bb84fab27782181d63d8c8f7ded958948afeb2d0.png)
A function to compute this Gaussian for arbitrary  and
and
 is also available ( signal.gauss_spline ). The
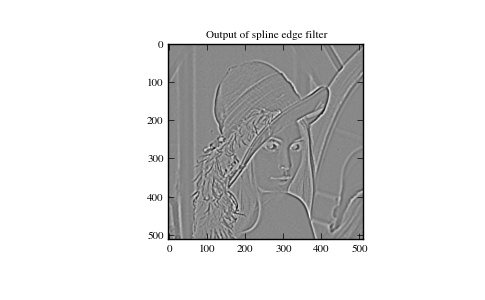
following code and Figure uses spline-filtering to compute an
edge-image (the second-derivative of a smoothed spline) of Lena’s face
which is an array returned by the command lena. The command
signal.sepfir2d was used to apply a separable two-dimensional
FIR filter with mirror- symmetric boundary conditions to the spline
coefficients. This function is ideally suited for reconstructing
samples from spline coefficients and is faster than
signal.convolve2d which convolves arbitrary two-dimensional
filters and allows for choosing mirror-symmetric boundary conditions.
is also available ( signal.gauss_spline ). The
following code and Figure uses spline-filtering to compute an
edge-image (the second-derivative of a smoothed spline) of Lena’s face
which is an array returned by the command lena. The command
signal.sepfir2d was used to apply a separable two-dimensional
FIR filter with mirror- symmetric boundary conditions to the spline
coefficients. This function is ideally suited for reconstructing
samples from spline coefficients and is faster than
signal.convolve2d which convolves arbitrary two-dimensional
filters and allows for choosing mirror-symmetric boundary conditions.
>>> from numpy import *
>>> from scipy import signal, misc
>>> import matplotlib.pyplot as plt
>>> image = misc.lena().astype(float32)
>>> derfilt = array([1.0,-2,1.0],float32)
>>> ck = signal.cspline2d(image,8.0)
>>> deriv = signal.sepfir2d(ck, derfilt, [1]) + \
>>> signal.sepfir2d(ck, [1], derfilt)
Alternatively we could have done:
laplacian = array([[0,1,0],[1,-4,1],[0,1,0]],float32)
deriv2 = signal.convolve2d(ck,laplacian,mode='same',boundary='symm')
>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(deriv)
>>> plt.gray()
>>> plt.title('Output of spline edge filter')
>>> plt.show()
Filtering¶
Filtering is a generic name for any system that modifies an input
signal in some way. In SciPy a signal can be thought of as a Numpy
array. There are different kinds of filters for different kinds of
operations. There are two broad kinds of filtering operations: linear
and non-linear. Linear filters can always be reduced to multiplication
of the flattened Numpy array by an appropriate matrix resulting in
another flattened Numpy array. Of course, this is not usually the best
way to compute the filter as the matrices and vectors involved may be
huge. For example filtering a  image with this
method would require multiplication of a
image with this
method would require multiplication of a 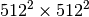 matrix with a
matrix with a 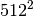 vector. Just trying to store the
vector. Just trying to store the
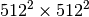 matrix using a standard Numpy array would
require
matrix using a standard Numpy array would
require 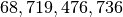 elements. At 4 bytes per element this
would require
elements. At 4 bytes per element this
would require 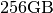 of memory. In most applications
most of the elements of this matrix are zero and a different method
for computing the output of the filter is employed.
of memory. In most applications
most of the elements of this matrix are zero and a different method
for computing the output of the filter is employed.
Convolution/Correlation¶
Many linear filters also have the property of shift-invariance. This means that the filtering operation is the same at different locations in the signal and it implies that the filtering matrix can be constructed from knowledge of one row (or column) of the matrix alone. In this case, the matrix multiplication can be accomplished using Fourier transforms.
Let ![x\left[n\right]](../_images/math/7a54a7c9d1c3adeb22199aa50a53aaed8f21c3e8.png) define a one-dimensional signal indexed by the
integer
define a one-dimensional signal indexed by the
integer 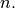 Full convolution of two one-dimensional signals can be
expressed as
Full convolution of two one-dimensional signals can be
expressed as
![\[ y\left[n\right]=\sum_{k=-\infty}^{\infty}x\left[k\right]h\left[n-k\right].\]](../_images/math/3983945b1984e9abdea8e3ae407f25bf1fa74978.png)
This equation can only be implemented directly if we limit the
sequences to finite support sequences that can be stored in a
computer, choose 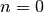 to be the starting point of both
sequences, let
to be the starting point of both
sequences, let 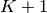 be that value for which
be that value for which
![y\left[n\right]=0](../_images/math/3647fe62a0b979c8d541d0dc7fb93b27e76ae9ad.png) for all
for all 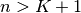 and
and 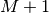 be
that value for which
be
that value for which ![x\left[n\right]=0](../_images/math/963d869ccb2c301bf4c6c0d31ac2b99c8d0e4a72.png) for all
for all 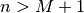 ,
then the discrete convolution expression is
,
then the discrete convolution expression is
![\[ y\left[n\right]=\sum_{k=\max\left(n-M,0\right)}^{\min\left(n,K\right)}x\left[k\right]h\left[n-k\right].\]](../_images/math/066721b94cf6ea5067af06b5a7b158dc11cdc08d.png)
For convenience assume  Then, more explicitly the output of
this operation is
Then, more explicitly the output of
this operation is
![\begin{eqnarray*} y\left[0\right] & = & x\left[0\right]h\left[0\right]\\ y\left[1\right] & = & x\left[0\right]h\left[1\right]+x\left[1\right]h\left[0\right]\\ y\left[2\right] & = & x\left[0\right]h\left[2\right]+x\left[1\right]h\left[1\right]+x\left[2\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[M\right] & = & x\left[0\right]h\left[M\right]+x\left[1\right]h\left[M-1\right]+\cdots+x\left[M\right]h\left[0\right]\\ y\left[M+1\right] & = & x\left[1\right]h\left[M\right]+x\left[2\right]h\left[M-1\right]+\cdots+x\left[M+1\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[K\right] & = & x\left[K-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[0\right]\\ y\left[K+1\right] & = & x\left[K+1-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[1\right]\\ \vdots & \vdots & \vdots\\ y\left[K+M-1\right] & = & x\left[K-1\right]h\left[M\right]+x\left[K\right]h\left[M-1\right]\\ y\left[K+M\right] & = & x\left[K\right]h\left[M\right].\end{eqnarray*}](../_images/math/6fe58cba92c006e7899b26eb7dd594b79b7a62d9.png)
Thus, the full discrete convolution of two finite sequences of lengths
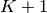 and
and 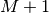 respectively results in a finite sequence of length
respectively results in a finite sequence of length
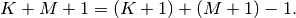
One dimensional convolution is implemented in SciPy with the function
signal.convolve . This function takes as inputs the signals
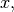
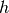 , and an optional flag and returns the signal
, and an optional flag and returns the signal
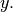 The optional flag allows for specification of which part of
the output signal to return. The default value of ‘full’ returns the
entire signal. If the flag has a value of ‘same’ then only the middle
The optional flag allows for specification of which part of
the output signal to return. The default value of ‘full’ returns the
entire signal. If the flag has a value of ‘same’ then only the middle
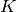 values are returned starting at
values are returned starting at ![y\left[\left\lfloor
\frac{M-1}{2}\right\rfloor \right]](../_images/math/868c62954a46d056df5db07d13ebbcdcbb4e3799.png) so that the output has the same
length as the largest input. If the flag has a value of ‘valid’ then
only the middle
so that the output has the same
length as the largest input. If the flag has a value of ‘valid’ then
only the middle 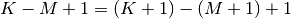 output values are returned where
output values are returned where  depends on all of the
values of the smallest input from
depends on all of the
values of the smallest input from ![h\left[0\right]](../_images/math/b745acac744f4de62b0672541590ac5e7187e6af.png) to
to
![h\left[M\right].](../_images/math/ef5c8ab9537368f5a0d8eb718c4a6c5b285b8d65.png) In other words only the values
In other words only the values
![y\left[M\right]](../_images/math/6355f12ed4c8290d438a4d55d7905a69d900eba6.png) to
to ![y\left[K\right]](../_images/math/e90cce44b1fd12ef749e98380080302c8bc83d2a.png) inclusive are
returned.
inclusive are
returned.
This same function signal.convolve can actually take 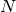 -dimensional arrays as inputs and will return the
-dimensional arrays as inputs and will return the 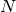 -dimensional convolution of the two arrays. The same input flags are
available for that case as well.
-dimensional convolution of the two arrays. The same input flags are
available for that case as well.
Correlation is very similar to convolution except for the minus sign becomes a plus sign. Thus
![\[ w\left[n\right]=\sum_{k=-\infty}^{\infty}y\left[k\right]x\left[n+k\right]\]](../_images/math/1c35c466421fa5230cbc3e308c3680d46fbf0015.png)
is the (cross) correlation of the signals 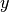 and
and 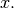 For
finite-length signals with
For
finite-length signals with ![y\left[n\right]=0](../_images/math/3647fe62a0b979c8d541d0dc7fb93b27e76ae9ad.png) outside of the range
outside of the range
![\left[0,K\right]](../_images/math/39088e750f5f05ddfcf7ba6f14cac3cd6a20f277.png) and
and ![x\left[n\right]=0](../_images/math/963d869ccb2c301bf4c6c0d31ac2b99c8d0e4a72.png) outside of the range
outside of the range
![\left[0,M\right],](../_images/math/d9f860be08db36284e9794517b69d0f8acaedd25.png) the summation can simplify to
the summation can simplify to
![\[ w\left[n\right]=\sum_{k=\max\left(0,-n\right)}^{\min\left(K,M-n\right)}y\left[k\right]x\left[n+k\right].\]](../_images/math/59652e6c1fc1470282728b83750bb245b511b77b.png)
Assuming again that  this is
this is
![\begin{eqnarray*} w\left[-K\right] & = & y\left[K\right]x\left[0\right]\\ w\left[-K+1\right] & = & y\left[K-1\right]x\left[0\right]+y\left[K\right]x\left[1\right]\\ \vdots & \vdots & \vdots\\ w\left[M-K\right] & = & y\left[K-M\right]x\left[0\right]+y\left[K-M+1\right]x\left[1\right]+\cdots+y\left[K\right]x\left[M\right]\\ w\left[M-K+1\right] & = & y\left[K-M-1\right]x\left[0\right]+\cdots+y\left[K-1\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[-1\right] & = & y\left[1\right]x\left[0\right]+y\left[2\right]x\left[1\right]+\cdots+y\left[M+1\right]x\left[M\right]\\ w\left[0\right] & = & y\left[0\right]x\left[0\right]+y\left[1\right]x\left[1\right]+\cdots+y\left[M\right]x\left[M\right]\\ w\left[1\right] & = & y\left[0\right]x\left[1\right]+y\left[1\right]x\left[2\right]+\cdots+y\left[M-1\right]x\left[M\right]\\ w\left[2\right] & = & y\left[0\right]x\left[2\right]+y\left[1\right]x\left[3\right]+\cdots+y\left[M-2\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[M-1\right] & = & y\left[0\right]x\left[M-1\right]+y\left[1\right]x\left[M\right]\\ w\left[M\right] & = & y\left[0\right]x\left[M\right].\end{eqnarray*}](../_images/math/6ce5f2d19a556c0a429cf5f242963542d31a2e61.png)
The SciPy function signal.correlate implements this
operation. Equivalent flags are available for this operation to return
the full 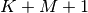 length sequence (‘full’) or a sequence with the
same size as the largest sequence starting at
length sequence (‘full’) or a sequence with the
same size as the largest sequence starting at
![w\left[-K+\left\lfloor \frac{M-1}{2}\right\rfloor \right]](../_images/math/61f32de921da939b4a1421ddcb79132aa5d25fe3.png) (‘same’) or a sequence where the values depend on all the values of
the smallest sequence (‘valid’). This final option returns the
(‘same’) or a sequence where the values depend on all the values of
the smallest sequence (‘valid’). This final option returns the
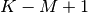 values
values ![w\left[M-K\right]](../_images/math/95c870f88b4ccd819a51eb06aec1a148b4fd9640.png) to
to
![w\left[0\right]](../_images/math/c59d75e227ea2f43ef26508669db8c2f2f209f6c.png) inclusive.
inclusive.
The function signal.correlate can also take arbitrary 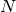 -dimensional arrays as input and return the
-dimensional arrays as input and return the 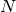 -dimensional
convolution of the two arrays on output.
-dimensional
convolution of the two arrays on output.
When  signal.correlate and/or
signal.convolve can be used to construct arbitrary image
filters to perform actions such as blurring, enhancing, and
edge-detection for an image.
signal.correlate and/or
signal.convolve can be used to construct arbitrary image
filters to perform actions such as blurring, enhancing, and
edge-detection for an image.
Convolution is mainly used for filtering when one of the signals is
much smaller than the other ( 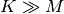 ), otherwise linear
filtering is more easily accomplished in the frequency domain (see
Fourier Transforms).
), otherwise linear
filtering is more easily accomplished in the frequency domain (see
Fourier Transforms).
Difference-equation filtering¶
A general class of linear one-dimensional filters (that includes convolution filters) are filters described by the difference equation
![\[ \sum_{k=0}^{N}a_{k}y\left[n-k\right]=\sum_{k=0}^{M}b_{k}x\left[n-k\right]\]](../_images/math/f17977ceb351f59b1be35c3ce49a259bdcc5b0c2.png)
where ![x\left[n\right]](../_images/math/7a54a7c9d1c3adeb22199aa50a53aaed8f21c3e8.png) is the input sequence and
is the input sequence and
![y\left[n\right]](../_images/math/c548a4b709772977ca62636c4ddc37d30a83c742.png) is the output sequence. If we assume initial
rest so that
is the output sequence. If we assume initial
rest so that ![y\left[n\right]=0](../_images/math/3647fe62a0b979c8d541d0dc7fb93b27e76ae9ad.png) for
for 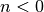 , then this
kind of filter can be implemented using convolution. However, the
convolution filter sequence
, then this
kind of filter can be implemented using convolution. However, the
convolution filter sequence ![h\left[n\right]](../_images/math/1dbbcdabd0912ad30c0a5001c4d06e389c1e19f9.png) could be infinite
if
could be infinite
if  for
for 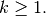 In addition, this general
class of linear filter allows initial conditions to be placed on
In addition, this general
class of linear filter allows initial conditions to be placed on
![y\left[n\right]](../_images/math/c548a4b709772977ca62636c4ddc37d30a83c742.png) for
for 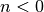 resulting in a filter that
cannot be expressed using convolution.
resulting in a filter that
cannot be expressed using convolution.
The difference equation filter can be thought of as finding
![y\left[n\right]](../_images/math/c548a4b709772977ca62636c4ddc37d30a83c742.png) recursively in terms of it’s previous values
recursively in terms of it’s previous values
![\[ a_{0}y\left[n\right]=-a_{1}y\left[n-1\right]-\cdots-a_{N}y\left[n-N\right]+\cdots+b_{0}x\left[n\right]+\cdots+b_{M}x\left[n-M\right].\]](../_images/math/a0522c6a15fc8f22c791aeb35b1bd68d51b21026.png)
Often 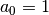 is chosen for normalization. The implementation
in SciPy of this general difference equation filter is a little more
complicated then would be implied by the previous equation. It is
implemented so that only one signal needs to be delayed. The actual
implementation equations are (assuming
is chosen for normalization. The implementation
in SciPy of this general difference equation filter is a little more
complicated then would be implied by the previous equation. It is
implemented so that only one signal needs to be delayed. The actual
implementation equations are (assuming 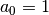 ).
).
![\begin{eqnarray*} y\left[n\right] & = & b_{0}x\left[n\right]+z_{0}\left[n-1\right]\\ z_{0}\left[n\right] & = & b_{1}x\left[n\right]+z_{1}\left[n-1\right]-a_{1}y\left[n\right]\\ z_{1}\left[n\right] & = & b_{2}x\left[n\right]+z_{2}\left[n-1\right]-a_{2}y\left[n\right]\\ \vdots & \vdots & \vdots\\ z_{K-2}\left[n\right] & = & b_{K-1}x\left[n\right]+z_{K-1}\left[n-1\right]-a_{K-1}y\left[n\right]\\ z_{K-1}\left[n\right] & = & b_{K}x\left[n\right]-a_{K}y\left[n\right],\end{eqnarray*}](../_images/math/062cff3bca754552673fdb66da28377d2bbd3d8c.png)
where 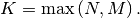 Note that
Note that 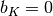 if
if
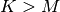 and
and 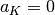 if
if 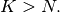 In this way, the
output at time
In this way, the
output at time 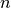 depends only on the input at time
depends only on the input at time 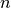 and the value of
and the value of 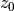 at the previous time. This can always
be calculated as long as the
at the previous time. This can always
be calculated as long as the 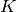 values
values
![z_{0}\left[n-1\right]\ldots z_{K-1}\left[n-1\right]](../_images/math/2a4b8eba8228f57bf3ec50a69e5b970a44125dab.png) are
computed and stored at each time step.
are
computed and stored at each time step.
The difference-equation filter is called using the command
signal.lfilter in SciPy. This command takes as inputs the
vector 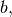 the vector,
the vector, 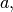 a signal
a signal  and
returns the vector
and
returns the vector 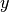 (the same length as
(the same length as  ) computed
using the equation given above. If
) computed
using the equation given above. If  is
is 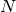 -dimensional, then the filter is computed along the axis provided. If,
desired, initial conditions providing the values of
-dimensional, then the filter is computed along the axis provided. If,
desired, initial conditions providing the values of
![z_{0}\left[-1\right]](../_images/math/13fa4765d1120308d98781a0c6d278e5895d3d25.png) to
to ![z_{K-1}\left[-1\right]](../_images/math/1568136cd65710bb52a9b44bf3b9dc0661c2f4a6.png) can be
provided or else it will be assumed that they are all zero. If initial
conditions are provided, then the final conditions on the intermediate
variables are also returned. These could be used, for example, to
restart the calculation in the same state.
can be
provided or else it will be assumed that they are all zero. If initial
conditions are provided, then the final conditions on the intermediate
variables are also returned. These could be used, for example, to
restart the calculation in the same state.
Sometimes it is more convenient to express the initial conditions in
terms of the signals ![x\left[n\right]](../_images/math/7a54a7c9d1c3adeb22199aa50a53aaed8f21c3e8.png) and
and
![y\left[n\right].](../_images/math/61a0760882b9f688928491ea6ef7a7fbe2a5818a.png) In other words, perhaps you have the values
of
In other words, perhaps you have the values
of ![x\left[-M\right]](../_images/math/e64b0f2e4c4fe7d20c557ab80665e7aee740196d.png) to
to ![x\left[-1\right]](../_images/math/d22f39bde126fcedae209972af2a6e0fd95e886b.png) and the values
of
and the values
of ![y\left[-N\right]](../_images/math/6536f83b0a5d0a31bbdd63153f942e9cb3e23d81.png) to
to ![y\left[-1\right]](../_images/math/1e3f1bb1d7e52040ce2ad7c86a800b9aece0ff15.png) and would like
to determine what values of
and would like
to determine what values of ![z_{m}\left[-1\right]](../_images/math/2e8083d91bba270fc7423dfa44f37a0fdcf53386.png) should be
delivered as initial conditions to the difference-equation filter. It
is not difficult to show that for
should be
delivered as initial conditions to the difference-equation filter. It
is not difficult to show that for 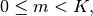
![\[ z_{m}\left[n\right]=\sum_{p=0}^{K-m-1}\left(b_{m+p+1}x\left[n-p\right]-a_{m+p+1}y\left[n-p\right]\right).\]](../_images/math/45c54ff2b4dadedf8b6b952453528407cc1a5ee3.png)
Using this formula we can find the intial condition vector
![z_{0}\left[-1\right]](../_images/math/13fa4765d1120308d98781a0c6d278e5895d3d25.png) to
to ![z_{K-1}\left[-1\right]](../_images/math/1568136cd65710bb52a9b44bf3b9dc0661c2f4a6.png) given initial
conditions on
given initial
conditions on 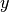 (and
(and  ). The command signal.lfiltic
performs this function.
). The command signal.lfiltic
performs this function.
Other filters¶
The signal processing package provides many more filters as well.
Median Filter¶
A median filter is commonly applied when noise is markedly non-Gaussian or when it is desired to preserve edges. The median filter works by sorting all of the array pixel values in a rectangular region surrounding the point of interest. The sample median of this list of neighborhood pixel values is used as the value for the output array. The sample median is the middle array value in a sorted list of neighborhood values. If there are an even number of elements in the neighborhood, then the average of the middle two values is used as the median. A general purpose median filter that works on N-dimensional arrays is signal.medfilt . A specialized version that works only for two-dimensional arrays is available as signal.medfilt2d .
Order Filter¶
A median filter is a specific example of a more general class of filters called order filters. To compute the output at a particular pixel, all order filters use the array values in a region surrounding that pixel. These array values are sorted and then one of them is selected as the output value. For the median filter, the sample median of the list of array values is used as the output. A general order filter allows the user to select which of the sorted values will be used as the output. So, for example one could choose to pick the maximum in the list or the minimum. The order filter takes an additional argument besides the input array and the region mask that specifies which of the elements in the sorted list of neighbor array values should be used as the output. The command to perform an order filter is signal.order_filter .
Wiener filter¶
The Wiener filter is a simple deblurring filter for denoising images.
This is not the Wiener filter commonly described in image
reconstruction problems but instead it is a simple, local-mean filter.
Let  be the input signal, then the output is
be the input signal, then the output is
![\[ y=\left\{ \begin{array}{cc} \frac{\sigma^{2}}{\sigma_{x}^{2}}m_{x}+\left(1-\frac{\sigma^{2}}{\sigma_{x}^{2}}\right)x & \sigma_{x}^{2}\geq\sigma^{2},\\ m_{x} & \sigma_{x}^{2}<\sigma^{2},\end{array}\right.\]](../_images/math/afb8c72cc93e5b7d8b9be98a50206b529f707f20.png)
where 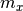 is the local estimate of the mean and
is the local estimate of the mean and
 is the local estimate of the variance. The
window for these estimates is an optional input parameter (default is
is the local estimate of the variance. The
window for these estimates is an optional input parameter (default is
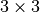 ). The parameter
). The parameter  is a threshold
noise parameter. If
is a threshold
noise parameter. If 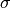 is not given then it is estimated
as the average of the local variances.
is not given then it is estimated
as the average of the local variances.
Hilbert filter¶
The Hilbert transform constructs the complex-valued analytic signal
from a real signal. For example if 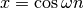 then
then
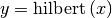 would return (except near the
edges)
would return (except near the
edges) 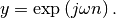 In the frequency domain,
the hilbert transform performs
In the frequency domain,
the hilbert transform performs
![\[ Y=X\cdot H\]](../_images/math/03a1bc7a1c56cccb67daa0fcbefbf19cf183f20f.png)
where 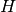 is 2 for positive frequencies,
is 2 for positive frequencies, 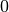 for negative
frequencies and
for negative
frequencies and 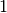 for zero-frequencies.
for zero-frequencies.
Least-Squares Spectral Analysis¶
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems.
Lomb-Scargle Periodograms (lombscargle)¶
The Lomb-Scargle method performs spectral analysis on unevenly sampled data and is known to be a powerful way to find, and test the significance of, weak periodic signals.
For a time series comprising 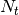 measurements
measurements
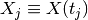 sampled at times
sampled at times 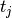 where
where
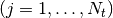 , assumed to have been scaled and shifted
such that its mean is zero and its variance is unity, the normalized
Lomb-Scargle periodogram at frequency
, assumed to have been scaled and shifted
such that its mean is zero and its variance is unity, the normalized
Lomb-Scargle periodogram at frequency 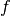 is
is
![P_{n}(f) \frac{1}{2}\left\{\frac{\left[\sum_{j}^{N_{t}}X_{j}\cos\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\cos^{2}\omega(t_{j}-\tau)}+\frac{\left[\sum_{j}^{N_{t}}X_{j}\sin\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\sin^{2}\omega(t_{j}-\tau)}\right\}.](../_images/math/e2f12448e0256da0a81704f415ebc4cb249d9f91.png)
Here, 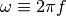 is the angular frequency.
The frequency dependent time offset
is the angular frequency.
The frequency dependent time offset 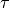 is given by
is given by
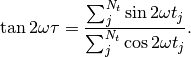
The lombscargle function calculates the periodogram using a slightly modified algorithm due to Townsend [3] which allows the periodogram to be calculated using only a single pass through the input arrays for each frequency.
The equation is refactored as:
![P_{n}(f) = \frac{1}{2}\left[\frac{(c_{\tau}XC + s_{\tau}XS)^{2}}{c_{\tau}^{2}CC + 2c_{\tau}s_{\tau}CS + s_{\tau}^{2}SS} + \frac{(c_{\tau}XS - s_{\tau}XC)^{2}}{c_{\tau}^{2}SS - 2c_{\tau}s_{\tau}CS + s_{\tau}^{2}CC}\right]](../_images/math/332bc1dc0147fbda5c3e741838a1cf5fb0dc1860.png)
and
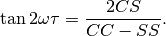
Here,

while the sums are
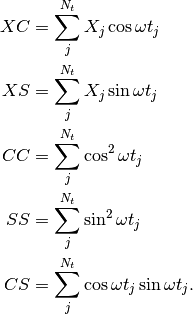
This requires 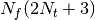 trigonometric function
evaluations giving a factor of
trigonometric function
evaluations giving a factor of 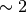 speed increase over the
straightforward implementation.
speed increase over the
straightforward implementation.
References
Some further reading and related software:
| [1] | N.R. Lomb “Least-squares frequency analysis of unequally spaced data”, Astrophysics and Space Science, vol 39, pp. 447-462, 1976 |
| [2] | J.D. Scargle “Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data”, The Astrophysical Journal, vol 263, pp. 835-853, 1982 |
| [3] | R.H.D. Townsend, “Fast calculation of the Lomb-Scargle periodogram using graphics processing units.”, The Astrophysical Journal Supplement Series, vol 191, pp. 247-253, 2010 |
