Maximum entropy models (scipy.maxentropy)¶
Warning
This module is deprecated in scipy 0.10, and will be removed in 0.11. Do not use this module in your new code. For questions about this deprecation, please ask on the scipy-dev mailing list.
Package content¶
Models:
| model([f, samplespace]) | A maximum-entropy (exponential-form) model on a discrete sample space. |
| bigmodel() | A maximum-entropy (exponential-form) model on a large sample space. |
| basemodel() | A base class providing generic functionality for both small and large maximum entropy models. |
| conditionalmodel(F, counts, numcontexts) | A conditional maximum-entropy (exponential-form) model p(x|w) on a discrete sample space. |
Utilities:
| arrayexp(x) | Returns the elementwise antilog of the real array x. |
| arrayexpcomplex | |
| columnmeans(A) | This is a wrapper for general dense or sparse dot products. |
| columnvariances(A) | This is a wrapper for general dense or sparse dot products. |
| densefeaturematrix | |
| densefeatures | |
| dotprod | |
| flatten(a) | Flattens the sparse matrix or dense array/matrix ‘a’ into a |
| innerprod(A, v) | This is a wrapper around general dense or sparse dot products. |
| innerprodtranspose(A, v) | This is a wrapper around general dense or sparse dot products. |
| logsumexp(a) | Compute the log of the sum of exponentials of input elements. |
| logsumexp_naive | |
| robustlog | |
| rowmeans | |
| sample_wr | |
| sparsefeaturematrix(f, sample[, format]) | Returns an (m x n) sparse matrix of non-zero evaluations of the scalar or vector functions f_1,...,f_m in the list f at the points x_1,...,x_n in the sequence ‘sample’. |
| sparsefeatures |
Usage information¶
Contains two classes for fitting maximum entropy models (also known as “exponential family” models) subject to linear constraints on the expectations of arbitrary feature statistics. One class, “model”, is for small discrete sample spaces, using explicit summation. The other, “bigmodel”, is for sample spaces that are either continuous (and perhaps high-dimensional) or discrete but too large to sum over, and uses importance sampling. conditional Monte Carlo methods.
The maximum entropy model has exponential form
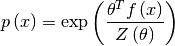
with a real parameter vector theta of the same length as the feature statistic f(x), For more background, see, for example, Cover and Thomas (1991), Elements of Information Theory.
See the file bergerexample.py for a walk-through of how to use these routines when the sample space is small enough to be enumerated.
See bergerexamplesimulated.py for a a similar walk-through using simulation.
