numpy.random.exponential

numpy.random.exponential(scale=1.0, size=None)

Exponential distribution.

Its probability density function is

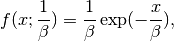
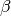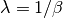for x > 0 and 0 elsewhere. is the scale parameter, which is the inverse of the rate parameter . The rate parameter is an alternative, widely used parameterization of the exponential distribution [R191].

The exponential distribution is a continuous analogue of the geometric distribution. It describes many common situations, such as the size of raindrops measured over many rainstorms [R189], or the time between page requests to Wikipedia [R190].

Parameters :

scale : float

The scale parameter, .

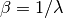size : tuple of ints

Number of samples to draw. The output is shaped according to size.

References

[R189]

(1, 2) Peyton Z. Peebles Jr., “Probability, Random Variables and Random Signal Principles”, 4th ed, 2001, p. 57.

[R190]

(1, 2) “Poisson Process”, Wikipedia, http://en.wikipedia.org/wiki/Poisson_process

[R191]

(1, 2) “Exponential Distribution, Wikipedia, http://en.wikipedia.org/wiki/Exponential_distribution