numpy.polynomial.chebyshev.chebint

numpy.polynomial.chebyshev.chebint(c, m=1, k=[], lbnd=0, scl=1, axis=0)

Integrate a Chebyshev series.

Returns the Chebyshev series coefficients c integrated m times from lbnd along axis. At each iteration the resulting series is multiplied by scl and an integration constant, k, is added. The scaling factor is for use in a linear change of variable. (“Buyer beware”: note that, depending on what one is doing, one may want scl to be the reciprocal of what one might expect; for more information, see the Notes section below.) The argument c is an array of coefficients from low to high degree along each axis, e.g., [1,2,3] represents the series T_0 + 2*T_1 + 3*T_2 while [[1,2],[1,2]] represents 1*T_0(x)*T_0(y) + 1*T_1(x)*T_0(y) + 2*T_0(x)*T_1(y) + 2*T_1(x)*T_1(y) if axis=0 is x and axis=1 is y.

Parameters :

c : array_like

Array of Chebyshev series coefficients. If c is multidimensional the different axis correspond to different variables with the degree in each axis given by the corresponding index.

m : int, optional

Order of integration, must be positive. (Default: 1)

k : {[], list, scalar}, optional

Integration constant(s). The value of the first integral at zero is the first value in the list, the value of the second integral at zero is the second value, etc. If k == [] (the default), all constants are set to zero. If m == 1, a single scalar can be given instead of a list.

lbnd : scalar, optional

The lower bound of the integral. (Default: 0)

scl : scalar, optional

Following each integration the result is multiplied by scl before the integration constant is added. (Default: 1)

axis : int, optional

Axis over which the integral is taken. (Default: 0).

New in version 1.7.0.

Returns :

S : ndarray

C-series coefficients of the integral.

Raises :

ValueError :

If m < 1, len(k) > m, np.isscalar(lbnd) == False, or np.isscalar(scl) == False.

See also

chebder

Notes

Note that the result of each integration is multiplied by scl. Why is this important to note? Say one is making a linear change of variable 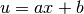in an integral relative to x. Then .. math::dx = du/a, so one will need to set scl equal to 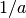- perhaps not what one would have first thought.

Also note that, in general, the result of integrating a C-series needs to be “reprojected” onto the C-series basis set. Thus, typically, the result of this function is “unintuitive,” albeit correct; see Examples section below.

Examples

>>> from numpy.polynomial import chebyshev as C
>>> c = (1,2,3)
>>> C.chebint(c)
array([ 0.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,3)
array([ 0.03125   , -0.1875    ,  0.04166667, -0.05208333,  0.01041667,
        0.00625   ])
>>> C.chebint(c, k=3)
array([ 3.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,lbnd=-2)
array([ 8.5, -0.5,  0.5,  0.5])
>>> C.chebint(c,scl=-2)
array([-1.,  1., -1., -1.])