numpy.linalg.pinv

numpy.linalg.pinv(a, rcond=1e-15)

Compute the (Moore-Penrose) pseudo-inverse of a matrix.

Calculate the generalized inverse of a matrix using its singular-value decomposition (SVD) and including all large singular values.

Parameters :

a : (M, N) array_like

Matrix to be pseudo-inverted.

rcond : float

Cutoff for small singular values. Singular values smaller (in modulus) than rcond * largest_singular_value (again, in modulus) are set to zero.

Returns :

B : (N, M) ndarray

The pseudo-inverse of a. If a is a matrix instance, then so is B.

Raises :

LinAlgError :

If the SVD computation does not converge.

Notes

The pseudo-inverse of a matrix A, denoted 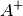, is defined as: “the matrix that ‘solves’ [the least-squares problem] 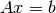,” i.e., if 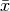is said solution, then 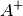is that matrix such that .

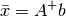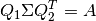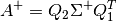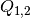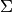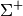It can be shown that if is the singular value decomposition of A, then , where are orthogonal matrices, is a diagonal matrix consisting of A’s so-called singular values, (followed, typically, by zeros), and then is simply the diagonal matrix consisting of the reciprocals of A’s singular values (again, followed by zeros). [R40]

References

[R40]

(1, 2) G. Strang, Linear Algebra and Its Applications, 2nd Ed., Orlando, FL, Academic Press, Inc., 1980, pp. 139-142.

Examples

The following example checks that a * a+ * a == a and a+ * a * a+ == a+:

>>> a = np.random.randn(9, 6)
>>> B = np.linalg.pinv(a)
>>> np.allclose(a, np.dot(a, np.dot(B, a)))
True
>>> np.allclose(B, np.dot(B, np.dot(a, B)))
True