numpy.linalg.lstsq

numpy.linalg.lstsq(a, b, rcond=-1)

Return the least-squares solution to a linear matrix equation.

Solves the equation a x = b by computing a vector x that minimizes the Euclidean 2-norm || b - a x ||^2. The equation may be under-, well-, or over- determined (i.e., the number of linearly independent rows of a can be less than, equal to, or greater than its number of linearly independent columns). If a is square and of full rank, then x (but for round-off error) is the “exact” solution of the equation.

Parameters :

a : (M, N) array_like

“Coefficient” matrix.

b : {(M,), (M, K)} array_like

Ordinate or “dependent variable” values. If b is two-dimensional, the least-squares solution is calculated for each of the K columns of b.

rcond : float, optional

Cut-off ratio for small singular values of a. Singular values are set to zero if they are smaller than rcond times the largest singular value of a.

Returns :

x : {(M,), (M, K)} ndarray

Least-squares solution. The shape of x depends on the shape of b.

residuals : {(), (1,), (K,)} ndarray

Sums of residuals; squared Euclidean 2-norm for each column in b - a*x. If the rank of a is < N or > M, this is an empty array. If b is 1-dimensional, this is a (1,) shape array. Otherwise the shape is (K,).

rank : int

Rank of matrix a.

s : (min(M, N),) ndarray

Singular values of a.

Raises :

LinAlgError :

If computation does not converge.

Notes

If b is a matrix, then all array results are returned as matrices.

Examples

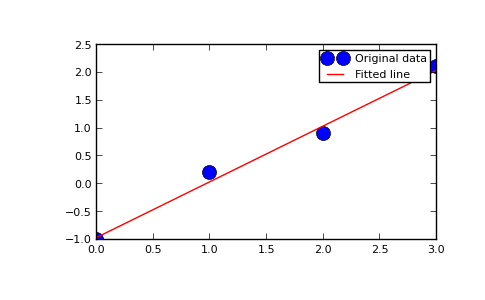
Fit a line, y = mx + c, through some noisy data-points:

>>> x = np.array([0, 1, 2, 3])
>>> y = np.array([-1, 0.2, 0.9, 2.1])

By examining the coefficients, we see that the line should have a gradient of roughly 1 and cut the y-axis at, more or less, -1.

We can rewrite the line equation as y = Ap, where A = [[x 1]] and p = [[m], [c]]. Now use lstsq to solve for p:

>>> A = np.vstack([x, np.ones(len(x))]).T
>>> A
array([[ 0.,  1.],
       [ 1.,  1.],
       [ 2.,  1.],
       [ 3.,  1.]])

>>> m, c = np.linalg.lstsq(A, y)[0]
>>> print m, c
1.0 -0.95

Plot the data along with the fitted line:

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o', label='Original data', markersize=10)
>>> plt.plot(x, m*x + c, 'r', label='Fitted line')
>>> plt.legend()
>>> plt.show()

(Source code, png, pdf)