numpy.cov

numpy.cov(m, y=None, rowvar=1, bias=0, ddof=None)

Estimate a covariance matrix, given data.

Covariance indicates the level to which two variables vary together. If we examine N-dimensional samples, , then the covariance matrix element 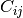is the covariance of 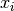and 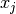. The element 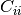is the variance of .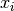

Parameters :

m : array_like

A 1-D or 2-D array containing multiple variables and observations. Each row of m represents a variable, and each column a single observation of all those variables. Also see rowvar below.

y : array_like, optional

An additional set of variables and observations. y has the same form as that of m.

rowvar : int, optional

If rowvar is non-zero (default), then each row represents a variable, with observations in the columns. Otherwise, the relationship is transposed: each column represents a variable, while the rows contain observations.

bias : int, optional

Default normalization is by (N - 1), where N is the number of observations given (unbiased estimate). If bias is 1, then normalization is by N. These values can be overridden by using the keyword ddof in numpy versions >= 1.5.

ddof : int, optional

New in version 1.5.

If not None normalization is by (N - ddof), where N is the number of observations; this overrides the value implied by bias. The default value is None.

Returns :

out : ndarray

The covariance matrix of the variables.

See also

corrcoef

Normalized covariance matrix

Examples

Consider two variables, 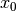and 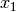, which correlate perfectly, but in opposite directions:

>>> x = np.array([[0, 2], [1, 1], [2, 0]]).T
>>> x
array([[0, 1, 2],
       [2, 1, 0]])

Note how 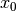increases while 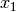decreases. The covariance matrix shows this clearly:

>>> np.cov(x)
array([[ 1., -1.],
       [-1.,  1.]])

Note that element 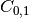, which shows the correlation between 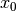and 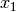, is negative.

Further, note how x and y are combined:

>>> x = [-2.1, -1,  4.3]
>>> y = [3,  1.1,  0.12]
>>> X = np.vstack((x,y))
>>> print np.cov(X)
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>> print np.cov(x, y)
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>> print np.cov(x)
11.71