numpy.random.logistic

numpy.random.logistic(loc=0.0, scale=1.0, size=None)

Draw samples from a Logistic distribution.

Samples are drawn from a Logistic distribution with specified parameters, loc (location or mean, also median), and scale (>0).

Parameters :

loc : float

scale : float > 0.

size : {tuple, int}

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns :

samples : {ndarray, scalar}

where the values are all integers in [0, n].

See also

scipy.stats.distributions.logistic

probability density function, distribution or cumulative density function, etc.

Notes

The probability density for the Logistic distribution is

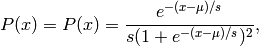
where 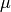= location and = scale.

The Logistic distribution is used in Extreme Value problems where it can act as a mixture of Gumbel distributions, in Epidemiology, and by the World Chess Federation (FIDE) where it is used in the Elo ranking system, assuming the performance of each player is a logistically distributed random variable.

References

[R82]

Reiss, R.-D. and Thomas M. (2001), Statistical Analysis of Extreme Values, from Insurance, Finance, Hydrology and Other Fields, Birkhauser Verlag, Basel, pp 132-133.

[R83]

Weisstein, Eric W. “Logistic Distribution.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/LogisticDistribution.html

[R84]

Wikipedia, “Logistic-distribution”, http://en.wikipedia.org/wiki/Logistic-distribution

Examples

Draw samples from the distribution:

>>> loc, scale = 10, 1
>>> s = np.random.logistic(loc, scale, 10000)
>>> count, bins, ignored = plt.hist(s, bins=50)

# plot against distribution

>>> def logist(x, loc, scale):
...     return exp((loc-x)/scale)/(scale*(1+exp((loc-x)/scale))**2)
>>> plt.plot(bins, logist(bins, loc, scale)*count.max()/\
... logist(bins, loc, scale).max())
>>> plt.show()