numpy.random.multivariate_normal

numpy.random.multivariate_normal(mean, cov[, size])

Draw random samples from a multivariate normal distribution.

The multivariate normal, multinormal or Gaussian distribution is a generalisation of the one-dimensional normal distribution to higher dimensions.

Such a distribution is specified by its mean and covariance matrix, which are analogous to the mean (average or “centre”) and variance (standard deviation squared or “width”) of the one-dimensional normal distribution.

Parameters:

mean : (N,) ndarray

Mean of the N-dimensional distribution.

cov : (N,N) ndarray

Covariance matrix of the distribution.

size : tuple of ints, optional

Given a shape of, for example, (m,n,k), m*n*k samples are generated, and packed in an m-by-n-by-k arrangement. Because each sample is N-dimensional, the output shape is (m,n,k,N). If no shape is specified, a single sample is returned.

Returns:

out : ndarray

The drawn samples, arranged according to size. If the shape given is (m,n,...), then the shape of out is is (m,n,...,N).

In other words, each entry out[i,j,...,:] is an N-dimensional value drawn from the distribution.

Notes

The mean is a coordinate in N-dimensional space, which represents the location where samples are most likely to be generated. This is analogous to the peak of the bell curve for the one-dimensional or univariate normal distribution.

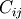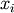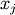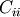Covariance indicates the level to which two variables vary together. From the multivariate normal distribution, we draw N-dimensional samples, . The covariance matrix element is the covariance of and . The element is the variance of 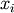(i.e. its “spread”).

Instead of specifying the full covariance matrix, popular approximations include:

• Spherical covariance (cov is a multiple of the identity matrix)
• Diagonal covariance (cov has non-negative elements, and only on the diagonal)

This geometrical property can be seen in two dimensions by plotting generated data-points:

>>> mean = [0,0]
>>> cov = [[1,0],[0,100]] # diagonal covariance, points lie on x or y-axis

>>> import matplotlib.pyplot as plt
>>> x,y = np.random.multivariate_normal(mean,cov,5000).T
>>> plt.plot(x,y,'x'); plt.axis('equal'); plt.show()

Note that the covariance matrix must be non-negative definite.

References

[84]	A. Papoulis, “Probability, Random Variables, and Stochastic Processes,” 3rd ed., McGraw-Hill Companies, 1991

[85]	R.O. Duda, P.E. Hart, and D.G. Stork, “Pattern Classification,” 2nd ed., Wiley, 2001.

Examples

>>> mean = (1,2)
>>> cov = [[1,0],[1,0]]
>>> x = np.random.multivariate_normal(mean,cov,(3,3))
>>> x.shape
(3, 3, 2)

The following is probably true, given that 0.6 is roughly twice the standard deviation:

>>> print list( (x[0,0,:] - mean) < 0.6 )
[True, True]