numpy.poly1d

class numpy.poly1d(c_or_r, r=0, variable=None)

A one-dimensional polynomial class.

Parameters:

c_or_r : array_like

Polynomial coefficients, in decreasing powers. For example, (1, 2, 3) implies 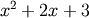. If r is set to True, these coefficients specify the polynomial roots (values where the polynomial evaluate to 0) instead.

r : bool, optional

If True, c_or_r gives the polynomial roots. Default is False.

Examples

Construct the polynomial :

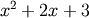>>> p = np.poly1d([1, 2, 3])
>>> print np.poly1d(p)
   2
1 x + 2 x + 3

Evaluate the polynomial:

>>> p(0.5)
4.25

Find the roots:

>>> p.r
array([-1.+1.41421356j, -1.-1.41421356j])

Show the coefficients:

>>> p.c
array([1, 2, 3])

Display the order (the leading zero-coefficients are removed):

>>> p.order
2

Show the coefficient of the k-th power in the polynomial (which is equivalent to p.c[-(i+1)]):

>>> p[1]
2

Polynomials can be added, substracted, multplied and divided (returns quotient and remainder):

>>> p * p
poly1d([ 1,  4, 10, 12,  9])

>>> (p**3 + 4) / p
(poly1d([  1.,   4.,  10.,  12.,   9.]), poly1d([4]))

asarray(p) gives the coefficient array, so polynomials can be used in all functions that accept arrays:

>>> p**2 # square of polynomial
poly1d([ 1,  4, 10, 12,  9])

>>> np.square(p) # square of individual coefficients
array([1, 4, 9])

The variable used in the string representation of p can be modified, using the variable parameter:

>>> p = np.poly1d([1,2,3], variable='z')
>>> print p
   2
1 z + 2 z + 3

Construct a polynomial from its roots:

>>> np.poly1d([1, 2], True)
poly1d([ 1, -3,  2])

This is the same polynomial as obtained by:

>>> np.poly1d([1, -1]) * np.poly1d([1, -2])
poly1d([ 1, -3,  2])