numpy.linalg.cholesky

numpy.linalg.cholesky(a)

Cholesky decomposition.

Return the Cholesky decomposition, 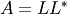of a Hermitian positive-definite matrix .

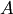Parameters:

a : array_like, shape (M, M)

Hermitian (symmetric, if it is real) and positive definite input matrix.

Returns:

L : array_like, shape (M, M)

Lower-triangular Cholesky factor of A.

Raises:

LinAlgError :

If the decomposition fails.

Notes

The Cholesky decomposition is often used as a fast way of solving

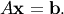
First, we solve for 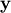in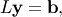

and then for 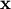in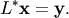

Examples

>>> A = np.array([[1,-2j],[2j,5]])
>>> L = np.linalg.cholesky(A)
>>> L
array([[ 1.+0.j,  0.+0.j],
       [ 0.+2.j,  1.+0.j]])
>>> np.dot(L, L.T.conj())
array([[ 1.+0.j,  0.-2.j],
       [ 0.+2.j,  5.+0.j]])