numpy.arctan

numpy.arctan(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'arctan'>

Trigonometric inverse tangent, element-wise.

The inverse of tan, so that if y = tan(x) then x = arctan(y).

Parameters:

x : array_like

out : ndarray, None, or tuple of ndarray and None, optional

A location into which the result is stored. If provided, it must have a shape that the inputs broadcast to. If not provided or None, a freshly-allocated array is returned. A tuple (possible only as a keyword argument) must have length equal to the number of outputs.

where : array_like, optional

This condition is broadcast over the input. At locations where the condition is True, the out array will be set to the ufunc result. Elsewhere, the out array will retain its original value. Note that if an uninitialized out array is created via the default out=None, locations within it where the condition is False will remain uninitialized.

**kwargs

For other keyword-only arguments, see the ufunc docs.

Returns:

out : ndarray or scalar

Out has the same shape as x. Its real part is in [-pi/2, pi/2] (arctan(+/-inf) returns +/-pi/2). This is a scalar if x is a scalar.

See also

arctan2

The “four quadrant” arctan of the angle formed by (x, y) and the positive x-axis.

angle

Argument of complex values.

Notes

arctan is a multi-valued function: for each x there are infinitely many numbers z such that tan(z) = x. The convention is to return the angle z whose real part lies in [-pi/2, pi/2].

For real-valued input data types, arctan always returns real output. For each value that cannot be expressed as a real number or infinity, it yields nan and sets the invalid floating point error flag.

For complex-valued input, arctan is a complex analytic function that has [1j, infj] and [-1j, -infj] as branch cuts, and is continuous from the left on the former and from the right on the latter.

The inverse tangent is also known as atan or tan^{-1}.

References

Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, 10th printing, New York: Dover, 1964, pp. 79. http://www.math.sfu.ca/~cbm/aands/

Examples

We expect the arctan of 0 to be 0, and of 1 to be pi/4:

>>> np.arctan([0, 1])
array([ 0.        ,  0.78539816])

>>> np.pi/4
0.78539816339744828

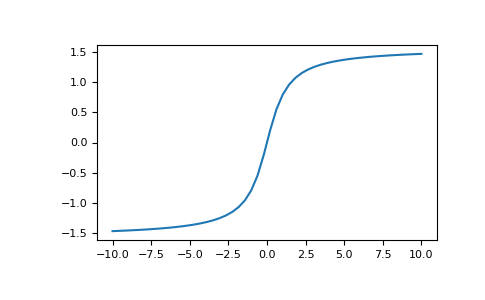
Plot arctan:

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-10, 10)
>>> plt.plot(x, np.arctan(x))
>>> plt.axis('tight')
>>> plt.show()