scipy.stats.

rv_discrete

class scipy.stats.rv_discrete(a=0, b=inf, name=None, badvalue=None, moment_tol=1e-08, values=None, inc=1, longname=None, shapes=None, seed=None)

A generic discrete random variable class meant for subclassing.

rv_discrete is a base class to construct specific distribution classes and instances for discrete random variables. It can also be used to construct an arbitrary distribution defined by a list of support points and corresponding probabilities.

Parameters:

afloat, optional

Lower bound of the support of the distribution, default: 0

bfloat, optional

Upper bound of the support of the distribution, default: plus infinity

moment_tolfloat, optional

The tolerance for the generic calculation of moments.

valuestuple of two array_like, optional

(xk, pk) where xk are integers and pk are the non-zero probabilities between 0 and 1 with sum(pk) = 1. xk and pk must have the same shape, and xk must be unique.

incinteger, optional

Increment for the support of the distribution. Default is 1. (other values have not been tested)

badvaluefloat, optional

The value in a result arrays that indicates a value that for which some argument restriction is violated, default is np.nan.

namestr, optional

The name of the instance. This string is used to construct the default example for distributions.

longnamestr, optional

This string is used as part of the first line of the docstring returned when a subclass has no docstring of its own. Note: longname exists for backwards compatibility, do not use for new subclasses.

shapesstr, optional

The shape of the distribution. For example “m, n” for a distribution that takes two integers as the two shape arguments for all its methods If not provided, shape parameters will be inferred from the signatures of the private methods, _pmf and _cdf of the instance.

seed{None, int, numpy.random.Generator, numpy.random.RandomState}, optional

If seed is None (or np.random), the numpy.random.RandomState singleton is used. If seed is an int, a new RandomState instance is used, seeded with seed. If seed is already a Generator or RandomState instance then that instance is used.

Attributes:

random_state

Get or set the generator object for generating random variates.

Methods

rvs(*args, **kwargs)	Random variates of given type.
pmf(k, *args, **kwds)	Probability mass function at k of the given RV.
logpmf(k, *args, **kwds)	Log of the probability mass function at k of the given RV.
cdf(k, *args, **kwds)	Cumulative distribution function of the given RV.
logcdf(k, *args, **kwds)	Log of the cumulative distribution function at k of the given RV.
sf(k, *args, **kwds)	Survival function (1 - cdf) at k of the given RV.
logsf(k, *args, **kwds)	Log of the survival function of the given RV.
ppf(q, *args, **kwds)	Percent point function (inverse of cdf) at q of the given RV.
isf(q, *args, **kwds)	Inverse survival function (inverse of sf) at q of the given RV.
moment(order, *args, **kwds)	non-central moment of distribution of specified order.
stats(*args, **kwds)	Some statistics of the given RV.
entropy(*args, **kwds)	Differential entropy of the RV.
expect([func, args, loc, lb, ub, ...])	Calculate expected value of a function with respect to the distribution for discrete distribution by numerical summation.
median(*args, **kwds)	Median of the distribution.
mean(*args, **kwds)	Mean of the distribution.
std(*args, **kwds)	Standard deviation of the distribution.
var(*args, **kwds)	Variance of the distribution.
interval(confidence, *args, **kwds)	Confidence interval with equal areas around the median.
__call__(*args, **kwds)	Freeze the distribution for the given arguments.
support(*args, **kwargs)	Support of the distribution.

Notes

This class is similar to rv_continuous. Whether a shape parameter is valid is decided by an _argcheck method (which defaults to checking that its arguments are strictly positive.) The main differences are as follows.

• The support of the distribution is a set of integers.

• Instead of the probability density function, pdf (and the corresponding private _pdf), this class defines the probability mass function, pmf (and the corresponding private _pmf.)

• There is no scale parameter.

• The default implementations of methods (e.g. _cdf) are not designed for distributions with support that is unbounded below (i.e. a=-np.inf), so they must be overridden.

To create a new discrete distribution, we would do the following:

>>> from scipy.stats import rv_discrete
>>> class poisson_gen(rv_discrete):
...     "Poisson distribution"
...     def _pmf(self, k, mu):
...         return exp(-mu) * mu**k / factorial(k)

and create an instance:

>>> poisson = poisson_gen(name="poisson")

Note that above we defined the Poisson distribution in the standard form. Shifting the distribution can be done by providing the loc parameter to the methods of the instance. For example, poisson.pmf(x, mu, loc) delegates the work to poisson._pmf(x-loc, mu).

Discrete distributions from a list of probabilities

Alternatively, you can construct an arbitrary discrete rv defined on a finite set of values xk with Prob{X=xk} = pk by using the values keyword argument to the rv_discrete constructor.

Deepcopying / Pickling

If a distribution or frozen distribution is deepcopied (pickled/unpickled, etc.), any underlying random number generator is deepcopied with it. An implication is that if a distribution relies on the singleton RandomState before copying, it will rely on a copy of that random state after copying, and np.random.seed will no longer control the state.

Examples

Try it in your browser!

Custom made discrete distribution:

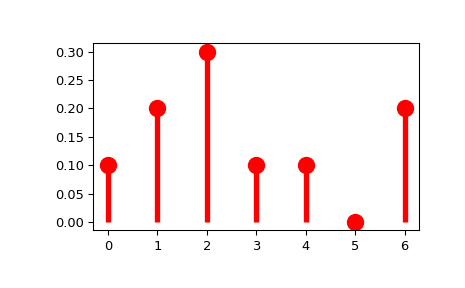
>>> import numpy as np
>>> from scipy import stats
>>> xk = np.arange(7)
>>> pk = (0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2)
>>> custm = stats.rv_discrete(name='custm', values=(xk, pk))
>>>
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.plot(xk, custm.pmf(xk), 'ro', ms=12, mec='r')
>>> ax.vlines(xk, 0, custm.pmf(xk), colors='r', lw=4)
>>> plt.show()

Random number generation:

>>> R = custm.rvs(size=100)

Go BackOpen In Tab