scipy.special.airy#
- scipy.special.airy(z, out=None) = <ufunc 'airy'>#
Airy functions and their derivatives.
- Parameters:
- zarray_like
Real or complex argument.
- outtuple of ndarray, optional
Optional output arrays for the function values
- Returns:
- Ai, Aip, Bi, Bip4-tuple of scalar or ndarray
Airy functions Ai and Bi, and their derivatives Aip and Bip.
See also
airyeexponentially scaled Airy functions.
Notes
The Airy functions Ai and Bi are two independent solutions of
\[y''(x) = x y(x).\]For real z in [-10, 10], the computation is carried out by calling the Cephes [1]
airyroutine, which uses power series summation for small z and rational minimax approximations for large z.Outside this range, the AMOS [2] zairy and zbiry routines are employed. They are computed using power series for \(|z| < 1\) and the following relations to modified Bessel functions for larger z (where \(t \equiv 2 z^{3/2}/3\)):
\[ \begin{align}\begin{aligned}Ai(z) = \frac{1}{\pi \sqrt{3}} K_{1/3}(t)\\Ai'(z) = -\frac{z}{\pi \sqrt{3}} K_{2/3}(t)\\Bi(z) = \sqrt{\frac{z}{3}} \left(I_{-1/3}(t) + I_{1/3}(t) \right)\\Bi'(z) = \frac{z}{\sqrt{3}} \left(I_{-2/3}(t) + I_{2/3}(t)\right)\end{aligned}\end{align} \]References
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
[2]Donald E. Amos, “AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order”, http://netlib.org/amos/
Examples
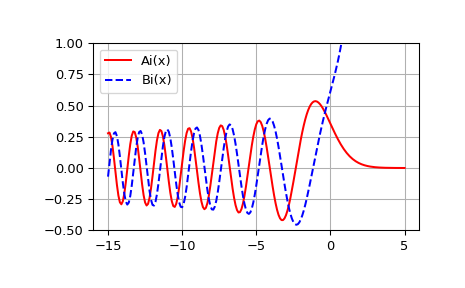
Compute the Airy functions on the interval [-15, 5].
>>> import numpy as np >>> from scipy import special >>> x = np.linspace(-15, 5, 201) >>> ai, aip, bi, bip = special.airy(x)
Plot Ai(x) and Bi(x).
>>> import matplotlib.pyplot as plt >>> plt.plot(x, ai, 'r', label='Ai(x)') >>> plt.plot(x, bi, 'b--', label='Bi(x)') >>> plt.ylim(-0.5, 1.0) >>> plt.grid() >>> plt.legend(loc='upper left') >>> plt.show()