scipy.interpolate.CloughTocher2DInterpolator#
- class scipy.interpolate.CloughTocher2DInterpolator(points, values, fill_value=nan, tol=1e-06, maxiter=400, rescale=False)#
CloughTocher2DInterpolator(points, values, tol=1e-6).
Piecewise cubic, C1 smooth, curvature-minimizing interpolator in 2D.
New in version 0.9.
- Parameters:
- pointsndarray of floats, shape (npoints, ndims); or Delaunay
2-D array of data point coordinates, or a precomputed Delaunay triangulation.
- valuesndarray of float or complex, shape (npoints, …)
N-D array of data values at points. The length of values along the first axis must be equal to the length of points. Unlike some interpolators, the interpolation axis cannot be changed.
- fill_valuefloat, optional
Value used to fill in for requested points outside of the convex hull of the input points. If not provided, then the default is
nan.- tolfloat, optional
Absolute/relative tolerance for gradient estimation.
- maxiterint, optional
Maximum number of iterations in gradient estimation.
- rescalebool, optional
Rescale points to unit cube before performing interpolation. This is useful if some of the input dimensions have incommensurable units and differ by many orders of magnitude.
See also
griddataInterpolate unstructured D-D data.
LinearNDInterpolatorPiecewise linear interpolator in N > 1 dimensions.
NearestNDInterpolatorNearest-neighbor interpolator in N > 1 dimensions.
interpnInterpolation on a regular grid or rectilinear grid.
RegularGridInterpolatorInterpolator on a regular or rectilinear grid in arbitrary dimensions (
interpnwraps this class).
Notes
The interpolant is constructed by triangulating the input data with Qhull [1], and constructing a piecewise cubic interpolating Bezier polynomial on each triangle, using a Clough-Tocher scheme [CT]. The interpolant is guaranteed to be continuously differentiable.
The gradients of the interpolant are chosen so that the curvature of the interpolating surface is approximatively minimized. The gradients necessary for this are estimated using the global algorithm described in [Nielson83] and [Renka84].
Note
For data on a regular grid use
interpninstead.References
[CT]See, for example, P. Alfeld, ‘’A trivariate Clough-Tocher scheme for tetrahedral data’’. Computer Aided Geometric Design, 1, 169 (1984); G. Farin, ‘’Triangular Bernstein-Bezier patches’’. Computer Aided Geometric Design, 3, 83 (1986).
[Nielson83]G. Nielson, ‘’A method for interpolating scattered data based upon a minimum norm network’’. Math. Comp., 40, 253 (1983).
[Renka84]R. J. Renka and A. K. Cline. ‘’A Triangle-based C1 interpolation method.’’, Rocky Mountain J. Math., 14, 223 (1984).
Examples
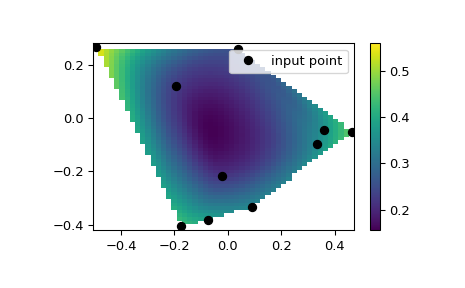
We can interpolate values on a 2D plane:
>>> from scipy.interpolate import CloughTocher2DInterpolator >>> import numpy as np >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> x = rng.random(10) - 0.5 >>> y = rng.random(10) - 0.5 >>> z = np.hypot(x, y) >>> X = np.linspace(min(x), max(x)) >>> Y = np.linspace(min(y), max(y)) >>> X, Y = np.meshgrid(X, Y) # 2D grid for interpolation >>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z) >>> Z = interp(X, Y) >>> plt.pcolormesh(X, Y, Z, shading='auto') >>> plt.plot(x, y, "ok", label="input point") >>> plt.legend() >>> plt.colorbar() >>> plt.axis("equal") >>> plt.show()
Methods
__call__(xi)Evaluate interpolator at given points.