Basic functions in Numpy (and top-level scipy)¶
Contents
Interaction with Numpy¶
To begin with, all of the Numpy functions have been subsumed into the scipy namespace so that all of those functions are available without additionally importing Numpy. In addition, the universal functions (addition, subtraction, division) have been altered to not raise exceptions if floating-point errors are encountered; instead, NaN’s and Inf’s are returned in the arrays. To assist in detection of these events, several functions (sp.isnan, sp.isfinite, sp.isinf) are available.
Finally, some of the basic functions like log, sqrt, and inverse trig functions have been modified to return complex numbers instead of NaN’s where appropriate (i.e. sp.sqrt(-1) returns 1j).
Top-level scipy routines¶
The purpose of the top level of scipy is to collect general-purpose routines that the other sub-packages can use and to provide a simple replacement for Numpy. Anytime you might think to import Numpy, you can import scipy instead and remove yourself from direct dependence on Numpy. These routines are divided into several files for organizational purposes, but they are all available under the numpy namespace (and the scipy namespace). There are routines for type handling and type checking, shape and matrix manipulation, polynomial processing, and other useful functions. Rather than giving a detailed description of each of these functions (which is available in the Numpy Reference Guide or by using the help, info and source commands), this tutorial will discuss some of the more useful commands which require a little introduction to use to their full potential.
Type handling¶
Note the difference between sp.iscomplex/sp.isreal and sp.iscomplexobj/sp.isrealobj. The former command is array based and returns byte arrays of ones and zeros providing the result of the element-wise test. The latter command is object based and returns a scalar describing the result of the test on the entire object.
Often it is required to get just the real and/or imaginary part of a complex number. While complex numbers and arrays have attributes that return those values, if one is not sure whether or not the object will be complex-valued, it is better to use the functional forms sp.real and sp.imag . These functions succeed for anything that can be turned into a Numpy array. Consider also the function sp.real_if_close which transforms a complex-valued number with tiny imaginary part into a real number.
Occasionally the need to check whether or not a number is a scalar (Python (long)int, Python float, Python complex, or rank-0 array) occurs in coding. This functionality is provided in the convenient function sp.isscalar which returns a 1 or a 0.
Finally, ensuring that objects are a certain Numpy type occurs often enough that it has been given a convenient interface in SciPy through the use of the sp.cast dictionary. The dictionary is keyed by the type it is desired to cast to and the dictionary stores functions to perform the casting. Thus, sp.cast['f'](d) returns an array of sp.float32 from d. This function is also useful as an easy way to get a scalar of a certain type:
>>> sp.cast['f'](sp.pi)
array(3.1415927410125732, dtype=float32)
Index Tricks¶
There are some class instances that make special use of the slicing functionality to provide efficient means for array construction. This part will discuss the operation of sp.mgrid , sp.ogrid , sp.r_ , and sp.c_ for quickly constructing arrays.
One familiar with MATLAB (R) may complain that it is difficult to construct arrays from the interactive session with Python. Suppose, for example that one wants to construct an array that begins with 3 followed by 5 zeros and then contains 10 numbers spanning the range -1 to 1 (inclusive on both ends). Before SciPy, you would need to enter something like the following
>>> concatenate(([3],[0]*5,arange(-1,1.002,2/9.0)))
With the r_ command one can enter this as
>>> r_[3,[0]*5,-1:1:10j]
which can ease typing and make for more readable code. Notice how objects are concatenated, and the slicing syntax is (ab)used to construct ranges. The other term that deserves a little explanation is the use of the complex number 10j as the step size in the slicing syntax. This non-standard use allows the number to be interpreted as the number of points to produce in the range rather than as a step size (note we would have used the long integer notation, 10L, but this notation may go away in Python as the integers become unified). This non-standard usage may be unsightly to some, but it gives the user the ability to quickly construct complicated vectors in a very readable fashion. When the number of points is specified in this way, the end- point is inclusive.
The “r” stands for row concatenation because if the objects between commas are 2 dimensional arrays, they are stacked by rows (and thus must have commensurate columns). There is an equivalent command c_ that stacks 2d arrays by columns but works identically to r_ for 1d arrays.
Another very useful class instance which makes use of extended slicing notation is the function mgrid. In the simplest case, this function can be used to construct 1d ranges as a convenient substitute for arange. It also allows the use of complex-numbers in the step-size to indicate the number of points to place between the (inclusive) end-points. The real purpose of this function however is to produce N, N-d arrays which provide coordinate arrays for an N-dimensional volume. The easiest way to understand this is with an example of its usage:
>>> mgrid[0:5,0:5]
array([[[0, 0, 0, 0, 0],
[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2],
[3, 3, 3, 3, 3],
[4, 4, 4, 4, 4]],
[[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4]]])
>>> mgrid[0:5:4j,0:5:4j]
array([[[ 0. , 0. , 0. , 0. ],
[ 1.6667, 1.6667, 1.6667, 1.6667],
[ 3.3333, 3.3333, 3.3333, 3.3333],
[ 5. , 5. , 5. , 5. ]],
[[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ]]])
Having meshed arrays like this is sometimes very useful. However, it is not always needed just to evaluate some N-dimensional function over a grid due to the array-broadcasting rules of Numpy and SciPy. If this is the only purpose for generating a meshgrid, you should instead use the function ogrid which generates an “open “grid using NewAxis judiciously to create N, N-d arrays where only one dimension in each array has length greater than 1. This will save memory and create the same result if the only purpose for the meshgrid is to generate sample points for evaluation of an N-d function.
Shape manipulation¶
In this category of functions are routines for squeezing out length- one dimensions from N-dimensional arrays, ensuring that an array is at least 1-, 2-, or 3-dimensional, and stacking (concatenating) arrays by rows, columns, and “pages “(in the third dimension). Routines for splitting arrays (roughly the opposite of stacking arrays) are also available.
Polynomials¶
There are two (interchangeable) ways to deal with 1-d polynomials in SciPy. The first is to use the poly1d class from Numpy. This class accepts coefficients or polynomial roots to initialize a polynomial. The polynomial object can then be manipulated in algebraic expressions, integrated, differentiated, and evaluated. It even prints like a polynomial:
>>> p = poly1d([3,4,5])
>>> print p
2
3 x + 4 x + 5
>>> print p*p
4 3 2
9 x + 24 x + 46 x + 40 x + 25
>>> print p.integ(k=6)
3 2
x + 2 x + 5 x + 6
>>> print p.deriv()
6 x + 4
>>> p([4,5])
array([ 69, 100])
The other way to handle polynomials is as an array of coefficients with the first element of the array giving the coefficient of the highest power. There are explicit functions to add, subtract, multiply, divide, integrate, differentiate, and evaluate polynomials represented as sequences of coefficients.
Vectorizing functions (vectorize)¶
One of the features that NumPy provides is a class vectorize to convert an ordinary Python function which accepts scalars and returns scalars into a “vectorized-function” with the same broadcasting rules as other Numpy functions (i.e. the Universal functions, or ufuncs). For example, suppose you have a Python function named addsubtract defined as:
>>> def addsubtract(a,b):
... if a > b:
... return a - b
... else:
... return a + b
which defines a function of two scalar variables and returns a scalar result. The class vectorize can be used to “vectorize “this function so that
>>> vec_addsubtract = vectorize(addsubtract)
returns a function which takes array arguments and returns an array result:
>>> vec_addsubtract([0,3,6,9],[1,3,5,7])
array([1, 6, 1, 2])
This particular function could have been written in vector form without the use of vectorize . But, what if the function you have written is the result of some optimization or integration routine. Such functions can likely only be vectorized using vectorize.
Other useful functions¶
There are several other functions in the scipy_base package including most of the other functions that are also in the Numpy package. The reason for duplicating these functions is to allow SciPy to potentially alter their original interface and make it easier for users to know how to get access to functions
>>> from scipy import *
Functions which should be mentioned are mod(x,y) which can replace x % y when it is desired that the result take the sign of y instead of x . Also included is fix which always rounds to the nearest integer towards zero. For doing phase processing, the functions angle, and unwrap are also useful. Also, the linspace and logspace functions return equally spaced samples in a linear or log scale. Finally, it’s useful to be aware of the indexing capabilities of Numpy. Mention should be made of the new function select which extends the functionality of where to include multiple conditions and multiple choices. The calling convention is select(condlist,choicelist,default=0). select is a vectorized form of the multiple if-statement. It allows rapid construction of a function which returns an array of results based on a list of conditions. Each element of the return array is taken from the array in a choicelist corresponding to the first condition in condlist that is true. For example
>>> x = r_[-2:3]
>>> x
array([-2, -1, 0, 1, 2])
>>> select([x > 3, x >= 0],[0,x+2])
array([0, 0, 2, 3, 4])
Common functions¶
Some functions depend on sub-packages of SciPy but should be available
from the top-level of SciPy due to their common use. These are
functions that might have been placed in scipy_base except for their
dependence on other sub-packages of SciPy. For example the
factorial and comb functions compute 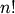 and
and
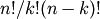 using either exact integer arithmetic (thanks to
Python’s Long integer object), or by using floating-point precision
and the gamma function. The functions rand and randn
are used so often that they warranted a place at the top level. There
are convenience functions for the interactive use: disp
(similar to print), and who (returns a list of defined
variables and memory consumption–upper bounded). Another function
returns a common image used in image processing: lena.
using either exact integer arithmetic (thanks to
Python’s Long integer object), or by using floating-point precision
and the gamma function. The functions rand and randn
are used so often that they warranted a place at the top level. There
are convenience functions for the interactive use: disp
(similar to print), and who (returns a list of defined
variables and memory consumption–upper bounded). Another function
returns a common image used in image processing: lena.
Finally, two functions are provided that are useful for approximating
derivatives of functions using discrete-differences. The function
central_diff_weights returns weighting coefficients for an
equally-spaced 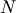 -point approximation to the derivative of
order o. These weights must be multiplied by the function
corresponding to these points and the results added to obtain the
derivative approximation. This function is intended for use when only
samples of the function are avaiable. When the function is an object
that can be handed to a routine and evaluated, the function
derivative can be used to automatically evaluate the object at
the correct points to obtain an N-point approximation to the o-th
derivative at a given point.
-point approximation to the derivative of
order o. These weights must be multiplied by the function
corresponding to these points and the results added to obtain the
derivative approximation. This function is intended for use when only
samples of the function are avaiable. When the function is an object
that can be handed to a routine and evaluated, the function
derivative can be used to automatically evaluate the object at
the correct points to obtain an N-point approximation to the o-th
derivative at a given point.
